B-Splines
Esta página describe cómo utilizar las B-splines en FreeCAD. También ofrece información sobre qué son las B-splines y para qué aplicaciones son útiles.
Motivación
Si ya conoces las B-splines y su aplicación, puedes continuar directamente con la sección B-splines en FreeCAD.
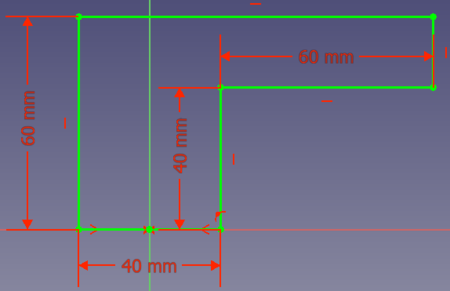
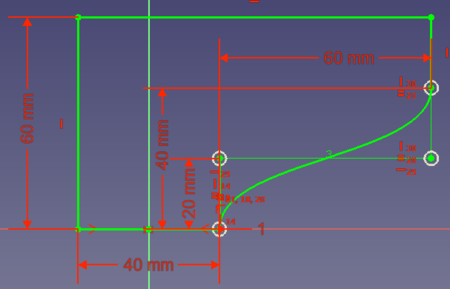
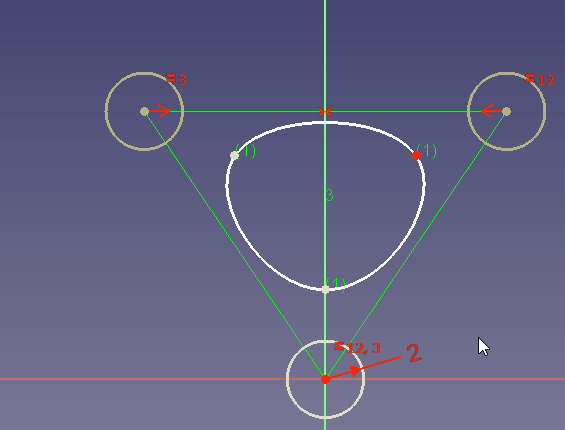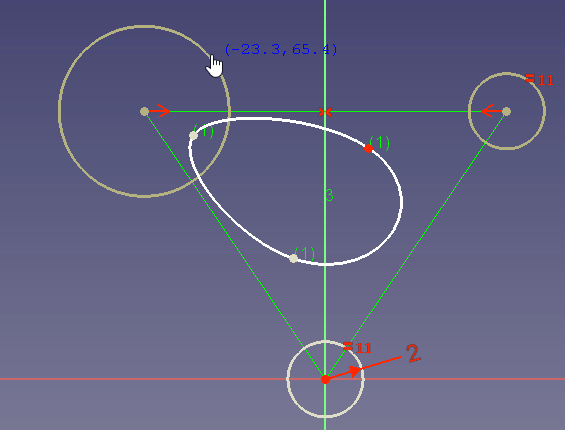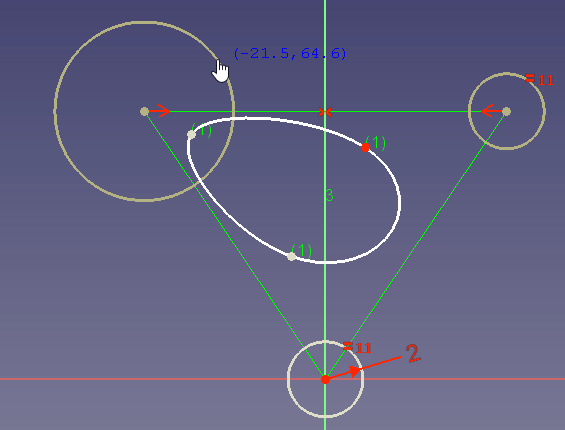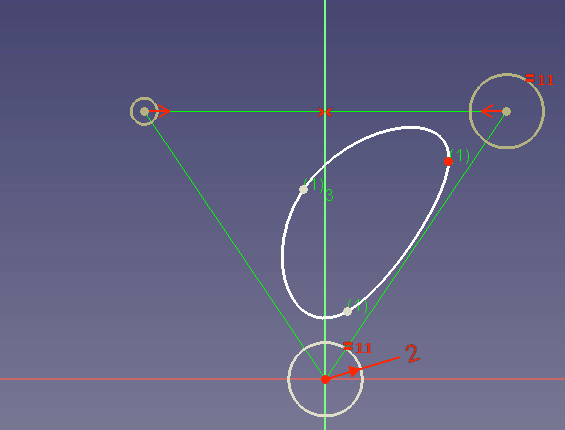
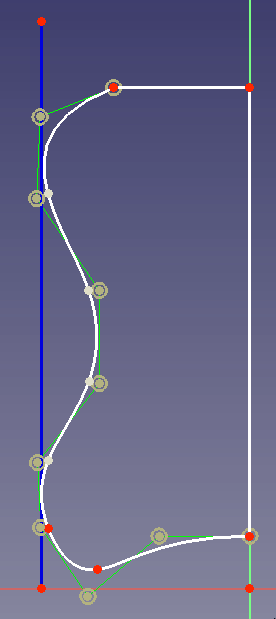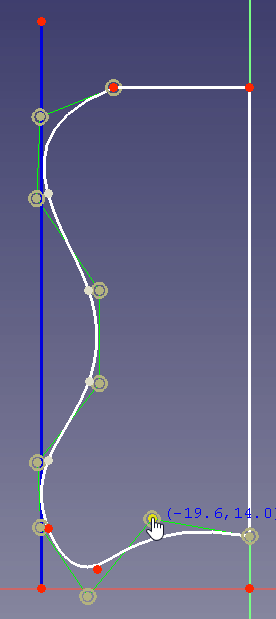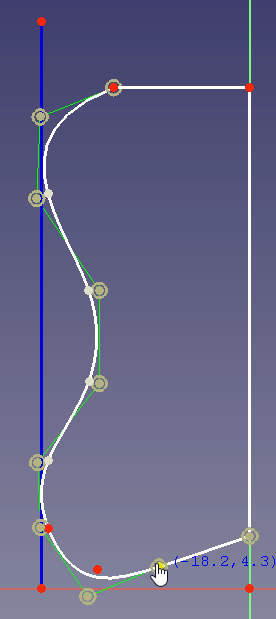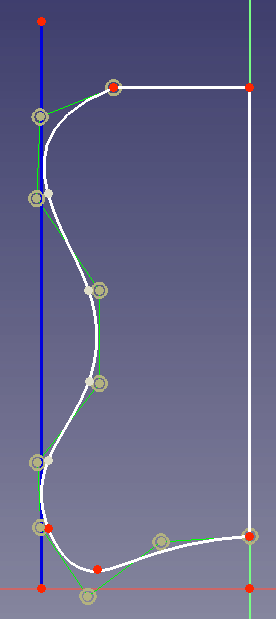
Supongamos que quiere diseñar una pieza que debe producirse con una impresora 3D. La pieza debe tener un borde de esta manera:
Hay que imprimir la pieza en dirección de la parte inferior del boceto hacia la parte superior. Las estructuras de soporte externas pueden no ser una opción. Por lo tanto, tiene que añadir un soporte directamente a su pieza. ¿Qué opciones tiene?
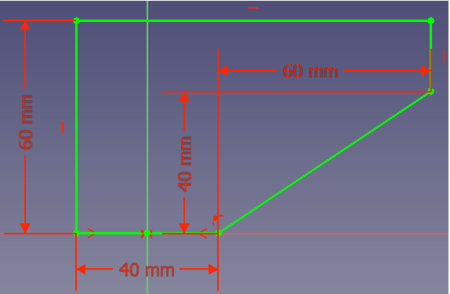
- Opción 1: se podría añadir una línea desde el punto (20, 0) hasta el punto (80, 40):
Sin embargo, esta solución necesita mucho volumen y, por tanto, peso y material.
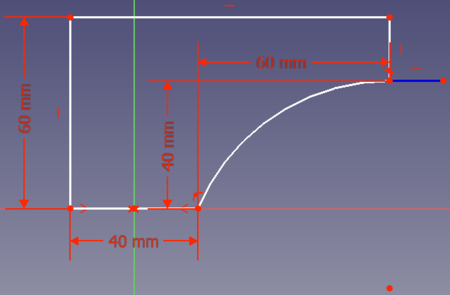
- Opción 2: puedes conectar los dos puntos con un arco de círculo. Para ahorrar volumen, el arco debe terminar tangencialmente en el punto (80,40). Entonces tu solución se ve así:
BIEN. Pero en el fondo no necesitas apoyo inmediato.
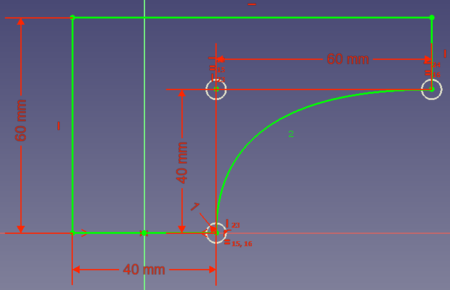
- Opción 3: se podría ahorrar algo más de volumen si la conexión entre los 2 puntos es una curva que empieza tangencialmente en (0, 20) y termina tangencialmente en (80, 40):
Así, una curva con la que se puedan conectar dos puntos tangencialmente a un punto de referencia puede ser muy útil para las construcciones. Las curvas de Bézier ofrecen esta característica.
Curvas Bézier
Derivación
Curvas de Bézier son polinomios que describen la conexión entre 2 puntos. El polinomio más sencillo que conecta 2 puntos es una recta () por lo que también las curvas de Bézier lineales son lineales:
Animación 1: Curva de Bézier lineal.
Sin embargo, un polinomio se vuelve primero útil cuando podemos controlarlo. Así que debe haber un punto entre los 2 puntos finales que nos permita definir cómo se conectan los puntos finales. Como en la opción 3 del ejemplo anterior, la curva es útil cuando comienza y termina tangencialmente a las líneas que cruzan los puntos finales. Y esta es una característica principal de las curvas Bézier. Así que vamos a añadir un punto de control entre los 2 puntos finales. La curva comenzará tangencialmente hacia este punto de control, lo que significa que es tangencial a la línea que podemos dibujar entre el punto inicial y el punto de control. Yendo hacia atrás desde el punto final, la curva también será tangente a la línea que podemos dibujar entre el punto de control y el punto final. La animación 2 muestra el aspecto de esta curva.
{{Caption|Animación 2: Curva cuadrática de Bézier. P1 es el punto de control.}
La animación aclara lo que es básicamente la curva: una transición de P0 a P2 al girar la línea P0-P1 para convertirse en la línea P1-P2. Por lo tanto, obtenemos la bonita característica de inicio/fin tangencial.
Una curva de este tipo sólo puede ser descrita por un polinomio cuadrático. (El número de vueltas a la izquierda/derecha + 1 es el orden necesario del polinomio. Un polinomio cuadrático tiene una sola vuelta, un polinomio cúbico tiene dos vueltas, y así sucesivamente). Por lo tanto, una curva de Bézier con un punto de control es una curva de Bézier cuadrática (de segundo orden).
Tener un solo punto de control a menudo no es suficiente. Tomemos el ejemplo de la motivación anterior. Allí, en la opción 3, terminamos la curva tangencialmente en la dirección x. ¿Pero cómo se pueden conectar los puntos (20, 0) y (80, 40) para que la curva termine tangencialmente en la dirección y? Para conseguirlo se necesita primero un giro a la derecha y luego a la izquierda, es decir, un polinomio cúbico (de tercer orden). Y eso significa que para una curva de Bézier necesitamos (o se puede decir que ganamos) un segundo punto de control. La animación 3 muestra una curva de Bézier cúbica.
Animación 3: Curva cúbica de Bézier.
Para responder a la pregunta, la solución con el final de la dirección y tangencial para el ejemplo es ésta:
Matemáticas
Si estás interesado en entender las matemáticas de fondo, aquí tienes lo básico.
Una curva de Bézier se calcula con esta fórmula:
n es por tanto el grado de la curva. Así, una curva de Bézier de grado n es un polígono de orden n. Los factores son, de hecho, las coordenadas de los puntos de control de las curvas de Bézier. Para una visualización, véase Control de las curvaturas de Bézier.
Si le interesa más, eche un vistazo a Las matemáticas de las curvas de Bézier con una derivación muy bien animada de las matemáticas de las curvas de Bézier.
Reglas
En el texto anterior ya habrás notado algunas "reglas" para las curvas de Bézier:
- El grado del polinomio es también el grado de las curvas.
- Si necesitas vueltas, necesitas al menos una curva de Bézier de grado.
- Una curva de Bézier siempre comienza tangencialmente a la línea entre el punto inicial y el primer punto de control (y termina tangencialmente a la línea entre el último punto de control y el punto final).
B-Splines
Básicos
Este vídeo enumera al principio los problemas prácticos de las curvas de Bézier. Por ejemplo, que al añadir o cambiar un punto de control se modifica toda la curva. Estos problemas se pueden resolver uniendo varias curvas de Bézier. El resultado es un llamado spline, en particular un B-spline (spline de base). El vídeo también explica que una unión de curvas de Bézier cuadráticas forma un B-spline cuadrático uniforme y que una unión de curvas de Bézier cúbicas forma un B-spline cúbico uniforme.
De los vídeos podemos recoger "reglas" útiles para las B-splines:
- El primer y último punto de control es el punto final/inicial de la spline.
- Al igual que para las curvas de Bézier, las splines siempre comienzan tangencialmente a la línea entre el punto de inicio y el primer punto de control (y terminan tangencialmente a la línea entre el último punto de control y el punto final).
- Una unión de curvas de Bézier con el grado tiene puntos de control.
- Dado que en la mayoría de los casos se trabaja con B-splines cúbicas podemos afirmar entonces que puntos de control conducen a segmentos de Bézier y a su vez puntos de unión de segmentos.
- Una B-spline de grado ofrece en cada punto una derivada continua de orden .
- Para una B-spline cúbica esto significa que la curvatura (derivada de segundo orden) no cambia al viajar de un segmento al siguiente. Esta es una característica muy útil como veremos más adelante.
Si está interesado en más detalles sobre las propiedades de la B-Spline, eche un vistazo al vídeo MOOC Curvas 8.2: Propiedades de las curvas B-spline.
Base
The name B-spline stands for Basis spline. Instead of forming the spline as a combination of Bézier curves, the approach is to to model the same spline a different way. The idea is hereby to use another set of polynomials as basis. A linear combination of these basis polynomials with the order forms the B-spline. This video explains the transition from the Bézier control points to the polynomial basis functions describing the spline. Mathematically we can describe a B-spline with this formula:
Hereby is the -th control point of the B-spline and also a factor for the -th base polynomial . Every basis polynomial describe the spline in a certain region and therefore moving a control point does not affect the whole spline. To understand this, it is highly recommended to have a look at this video starting at minute 2:23.
As explained in the video, the basis polynomials are Bernstein polynomials. The set of basis polynomials for a certain B-spline can be visualized this way:
A set of Bernstein polynomials with order 4. They describe a 4th order B-spline with 5 control points.
At every spline position the sum of polynomials is 1 (indicated by the orange line). At the start only the red polynomial has an influence since all other polynomials are there 0. At greater the spline is described by a linear combination of different basis polynomials. In the image above, every polynomial is greater than 1 for the whole range . This is not necessarily the case. As shown in the video, the basis polynomials are basically only greater than 0 for a certain spline position range. The interval at which a basis polynomial is greater than 0 is described by the knot vector. If you are interested in learning about the knot vector, have a look at this video.
B-splines no-uniformes
A property of the Bernstein polynomials is that when looking at the different S-spline Bézier parts, the path length of every part is the same. (The path length is often called the travel time). As you can imagine, it can be useful to have B-splines whose Bézier parts have different path lengths. This can be achieved by weighting the different polynomials:
is hereby the weight of the -th control point. When the weights are not equal, the B-spline is called non-uniform.
Especially when B-splines should be used for 3D modelling, normalized, non-uniform B-splines are necessary. The normalization is done by a division by the weighted basis functions. Thus when all are equal, we get a uniform B-spline, independent on the weight itself:
These non-uniform and rational (because of the division) B-splines are often called NURBS. Looking at their formula, we see that they are in fact a B-spline with a weighted basis :
whereas
B-splines en FreeCAD
FreeCAD ofrece la posibilidad de crear B-splines uniformes o no uniformes de cualquier grado en 2D a través del Ambiente de trabajo Croquizador.
Creación
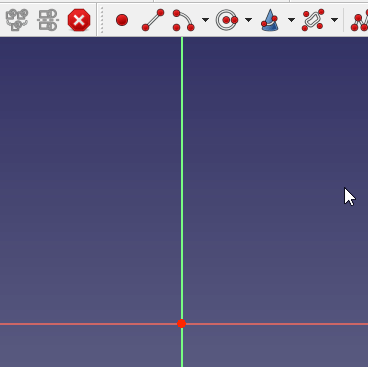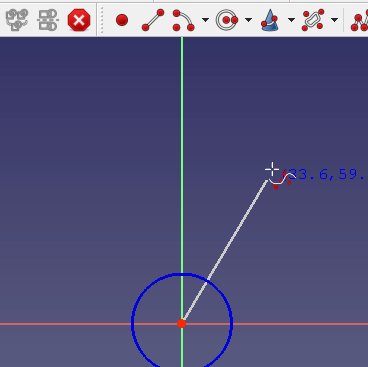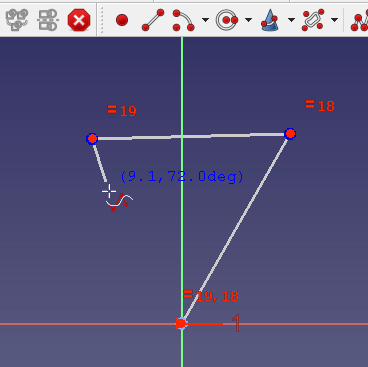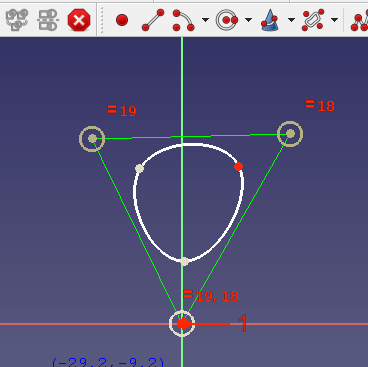
Para crear B-splines, entra en un sketch y utiliza el botón de la barra de herramientas Crear B-spline. A continuación, haz clic con el botón izquierdo para establecer un punto de control, mueve el ratón con el botón izquierdo para establecer el siguiente punto de control y así sucesivamente. Finalmente, haz clic con el botón derecho para terminar la definición y crear la B-spline.
Por defecto se crean splines cúbicas uniformes, excepto que no hay suficientes puntos de control para hacerlo. Así que cuando se crea una B-splinecon sólo 2 puntos de control, se obtiene por supuesto una spline que es curva lineal simple de Bézier, para 3 puntos de control se obtiene una curva cuadrática de Bézier, primero con 5 puntos de control se obtiene una spline B cúbica que consiste en 2 segmentos de Bézier.
Para crear B-splines periódicas (B-splines que forman una curva cerrada), utiliza el botón de la barra de herramientas Template:Botón. No es necesario fijar el último punto de control sobre el primero porque la B-spline se cerrará automáticamente:
Las B-splines también pueden generarse a partir de segmentos de croquis existentes. Para ello, seleccione los elementos y pulse el botón de la barra de herramientas Convertir geometría en B-spline.
Cambio de grado
To change the degree, select the B-spline and use either the toolbar button Increase B-spline degree or
Decrease B-spline degree.
Note: Decreasing the degree cannot revert a prior increase of the degree, see the Wiki page Decrease B-spline degree for an explanation.
Cambiar la multiplicidad de nudos
The points where two Bézier curves are connected to form the B-spline are called knots. The knot multiplicity determines how the Bézier parts are connected, see the Wiki page Increase knot multiplicity for details.
To change the knot multiplicity, use the toolbar buttons B-spline increase knot multiplicity or
B-spline decrease knot multiplicity.
Note: Creating two B-Splines that are connected to each other will not unite to a single new B-spline. So their connection point is not a knot. The only way to get a new knot in an existing B-spline is to decrease the degree. However, you may get many new knots. Thus the better choice is to redraw the B-spline with more control points.
Cambiar el peso
Around every control point you see a dark yellow circle. Its radius sets the weight for the corresponding control point. By default all circles have the radius 1. This is indicated with a radius constraint for the first control point circle.
To create a non-uniform B-spline the weights have to be non-uniform. To achieve that you can either change the radius constraint of the first control point circle:
File:Sketcher Changing-control-point-weigth-constraint.gif
or you delete the constraint that all circles are equal and then set different radius constraints for the circles.
If no radius constraint is set, you can also change the radius by dragging:
In the dragging example you see that a high weight attracts the curve to the control point while a very low weight changes the curve so as if the control point does almost not exist.
When you look at the creation function for non-uniform rational B-splines you see that a weight of zero would lead to a division by zero. Therefore you can only specify weights greater than zero.
Mostrar Información
Since the form of a B-spline does not tell much about its properties, FreeCAD offers different tools to display the properties:
| Property | Toolbar button |
| Degree | |
| Control polygon | |
| Curvature comb | |
| Knot multiplicity | |
| Weights |
Limitaciones
At the moment (FreeCAD 0.19) there are some limitations when using splines you should know:
- You cannot set tangential constraints.
In this example
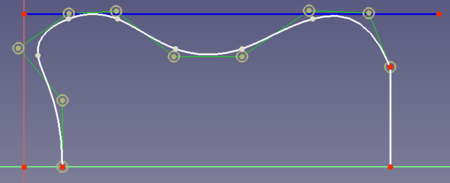
you want to assure that the spline touches the blue curve 2 times tangentially. This would be useful because the blue line could for example be the spatial border for your design. - You cannot insert a new control point between two selected existing control points. There is no other way than to redraw the spline.
- You cannot delete a control point. Also in this case you must redraw the spline
- You cannot create an offset curve for a B-spline using the tool Draft Offset.
Casos típicos de uso
Según las propiedades de las B-splines, hay 3 casos de uso principales:
- Curvas que comienzan/terminan tangencialmente a una determinada dirección. Un ejemplo de esto es el ejemplo de motivación arriba.
- Curvas que describen diseños más grandes y proporcionan la libertad de cambios locales. Véase este ejemplo más abajo.
- Curvas que proporcionan una cierta continuidad (derivada). Véase este ejemplo más abajo.
Diseño
Tomemos por ejemplo el caso de que usted diseñe la carcasa de una batidora de cocina. Su forma deseada debe ser como esta:
Para definir la forma exterior es ventajoso utilizar una B-spline porque cuando se cambia un punto de control para cambiar la curvatura en la parte inferior, la curvatura en el lado y la parte superior no se cambiará:
Continuidad en las transiciones geométricas
There are several cases where it is physically necessary to have a certain surface continuity at geometric transitions. Take for example the inner walls of a fluid channel. When you have a change in the diameter of the channel, you don't want to have an edge because edges would introduce turbulences. Therefore, like in the motivation example above, one uses splines for this purpose.
The development of the Bézier curves was initially triggered by the French car industry. Besides the saving of material and the reduction of the air flow drag, the look of the cars should also be improved. And when you look at the fancy design of French cars from the 60's and 70's you see that the Bézier curves gave car design a boost.
Let's take for example this task in the design of cars: The car fender should "look nice". Here is a basic sketch of our task:
"Looking nice" means that the (potential) customer looks at the fender and does not see unexpected light reflections and also no sudden changes in the reflection from the automotive paint at all. So what do you need to avoid changes in the reflections? Looking closely to the fender:
At the spatial area above the edge the intensity of reflected light is low (denoted by the red ellipse) because no light is directly reflected in the direction from the edge to the eye.
you see when there is an edge, there is a spatial area where the reflected light has less intensity and this is what you will notice when looking at the fender. To avoid this you need a continuous change in the slope of your surface elements. The slope is the first order derivative and as explained in section Basics, a second degree (quadratic) B-spline offers at every point a continuous first order derivative.
But is this really sufficient? At the point of geometric transition we have now at both sides the same slope, but the slope might change differently at both sides. Then we have this situation:
Por lo tanto, también tenemos zonas espaciales en las que la intensidad de la luz reflejada es diferente. Para evitar esto, necesitamos en el punto geométrico de transición también una continuidad de la derivada de segundo orden y, por tanto, una B-spline cúbica.