B-Splines/de: Difference between revisions
(Created page with "Im Augenblick (FreeCAD 0.19) gibt es einige Begrenzungen bei der Verwendung von Splines, die du kennen solltest: # Du kannst keine tangentialen Beschränkungen festlegen.</br>...") |
(Created page with "Entsprechend den Eigenschaften von B-Splines gibt es 3 Hauptanwendungsfälle: # Kurven, die tangential zu einer bestimmten Richtung beginnen/enden. Ein Beispiel hierfür ist d...") |
||
| Line 225: | Line 225: | ||
== Typische Anwendungsfälle == |
== Typische Anwendungsfälle == |
||
Entsprechend den Eigenschaften von B-Splines gibt es 3 Hauptanwendungsfälle: |
|||
According to the properties of B-splines, there are 3 main use cases: |
|||
# Kurven, die tangential zu einer bestimmten Richtung beginnen/enden. Ein Beispiel hierfür ist das Motivationsbeispiel [[#Motivation|oben]]. |
|||
# Curves that start/end tangentially to a certain direction. An example for this is the motivation example [[#Motivation|above]]. |
|||
# Kurven, die größere Entwürfe beschreiben und die Freiheit lokaler Änderungen bieten. Siehe [[#Gestaltung |dieses Beispiel]] unten. |
|||
# Curves describing larger designs and providing the freedom of local changes. See [[#Designing |this example]] below. |
|||
# Kurven, die eine gewisse Stetigkeit (Ableitung) bieten. Siehe [[#Stetigkeit an geometrischen Übergängen|dieses Beispiel]] unten. |
|||
# Curves providing a certain continuity (derivative). See [[#Continuity at Geometric Transitions|this example]] below. |
|||
=== Gestaltung === |
=== Gestaltung === |
||
Revision as of 08:37, 5 October 2021
Diese Seite beschreibt, wie man B-Splines in FreeCAD verwendet. Sie gibt auch Hintergrundinformationen, was B-Splines sind und für welche Anwendungen sie nützlich sind.
Motivation
Wenn du bereits über B-Splines und deren Anwendung Bescheid weisst, kannst du direkt mit dem Abschnitt B-Splines in FreeCAD fortfahren.
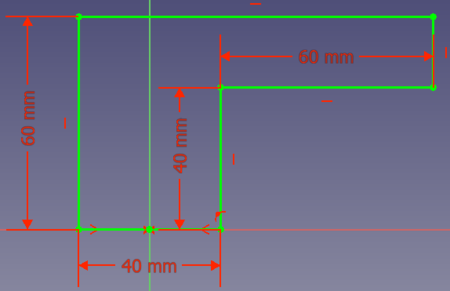
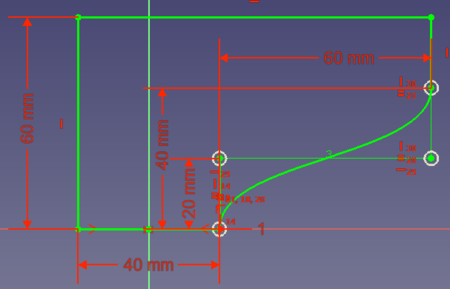
Nehmen wir an, Du willst ein Teil entwerfen, das mit einem 3D Drucker hergestellt werden soll. Das Teil muss so eine Kante haben:
Du musst das Teil in Richtung der Unterseite der Skizze nach oben drucken. Äußere Stützstrukturen sind möglicherweise keine Option. Daher musst Du eine Stütze direkt an deinem Teil anbringen. Welche Möglichkeiten hast du?
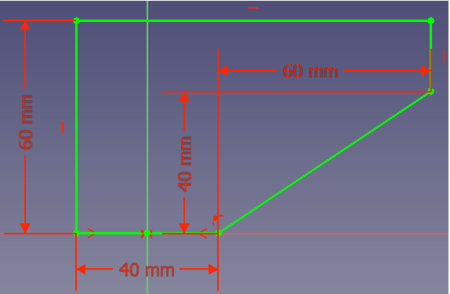
- Option 1: du kannst eine Linie vom Punkt (20, 0) zum Punkt (80, 40) hinzufügen:
Allerdings benötigt diese Lösung viel Volumen, also Gewicht und Material.
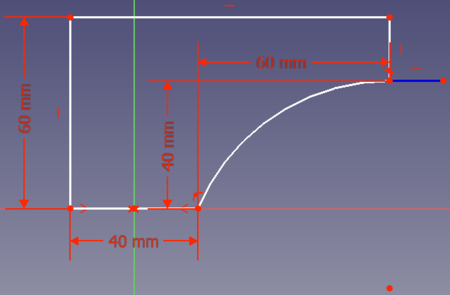
- Option 2: du kannst die beiden Punkte mit einem Kreisbogen verbinden. Um Volumen zu sparen, sollte der Bogen tangential im Punkt (80,40) enden. Dann sieht deine Lösung wie folgt aus:
GUT. Aber ganz unten brauchst du keine sofortige Unterstützung.
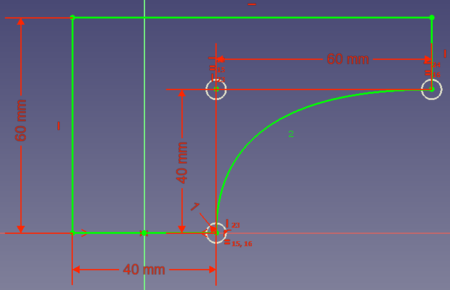
- Option 3: du kannst noch mehr Volumen einsparen, wenn die Verbindung zwischen den beiden Punkten eine Kurve wäre, die tangential bei (0, 20) beginnt und tangential bei (80, 40) endet:
So kann eine Kurve, mit der du zwei Punkte tangential zu einem Bezugspunkt verbinden kannst, sehr nützlich für Konstruktionen sein. Bézierkurven bieten diese Möglichkeit.
Bézierkurven
Herleitung
Bézierkurven sind Polynome zur Beschreibung der Verbindung zwischen 2 Punkten. Das einfachste Polynom, das 2 Punkte verbindet, ist eine Gerade (), daher sind auch lineare Bézierkurven linear:
Animation 1: Lineare Bézierkurve.
Ein Polynom wird jedoch erst dann nützlich, wenn wir es kontrollieren können. Es sollte also einen Punkt zwischen den beiden Endpunkten geben, der es uns erlaubt zu definieren, wie die Endpunkte verbunden sind. Wie im obigen Beispiel, Option 3, ist die Kurve hilfreich, wenn sie tangential zu Linien beginnt und endet, die die Endpunkte kreuzen. Und das ist ein Hauptmerkmal von Bézierkurven. Fügen wir also einen Kontrollpunkt zwischen den 2 Endpunkten ein. Die Kurve beginnt tangential zu diesem Kontrollpunkt, d. h. sie verläuft tangential zu der Linie, die wir zwischen dem Startpunkt und dem Kontrollpunkt ziehen können. Wenn man vom Endpunkt aus rückwärts geht, verläuft die Kurve ebenfalls tangential zu der Linie, die wir zwischen dem Kontrollpunkt und dem Endpunkt zeichnen können. Animation 2 zeigt, wie eine solche Kurve aussieht.
Animation 2: Quadratische Bézierkurve. P1 ist hierbei der Kontrollpunkt.
Die Animation verdeutlicht, worum es sich bei der Kurve im Grunde handelt - um einen Übergang von P0 zu P2, indem die Linie P0-P1 in die Linie P1-P2 gedreht wird. Dadurch erhalten wir das schöne tangentiale Anfang/Ende Merkmal.
Eine solche Kurve kann nur durch ein quadratisches Polynom beschrieben werden. (Die Anzahl der Links-/Rechtsdrehungen + 1 ist die erforderliche Polynomordnung. Ein quadratisches Polynom hat eine einzige Windung, ein kubisches Polynom hat zwei Windungen usw.) Daher ist eine Bézierkurve mit einem Kontrollpunkt eine quadratische Bézierkurve (zweiter Ordnung).
Ein einziger Kontrollpunkt ist oft nicht ausreichend. Nimm das obige Motivationsbeispiel. Bei der Option 3 endet die Kurve tangential in x-Richtung. Aber wie kann man die Punkte (20, 0) und (80, 40) so verbinden, dass die Kurve tangential in y-Richtung endet? Dazu braucht man erst eine Rechts- und dann eine Linkskurve, also ein kubisches Polynom (dritter Ordnung). Und das bedeutet für eine Bézierkurve, dass wir einen zweiten Kontrollpunkt brauchen (oder man kann sagen, wir gewinnen). Animation 3 zeigt eine kubische Bézierkurve.
Animation 3: Kubische Bézierkurve.
Um die Frage zu beantworten: Die Lösung mit dem tangentialen Ende in y-Richtung für das Beispiel ist diese:
Mathe
Wenn du an den mathematischen Hintergründen interessiert bist, hier sind die Grundlagen.
Eine Bézierkurve wird mit dieser Formel berechnet:
Dabei ist n der Grad der Kurve. Eine Bézierkurve vom Grad n ist also ein Polygon der Ordnung n. Die Faktoren sind dabei die Koordinaten der Kontrollpunkte der Bézierkurven. Zur Veranschaulichung siehe Steuerung von Bézierkurven.
Wenn du weiter interessiert bist, sieh dir Die Mathematik der Bézierkurven mit einer schön animierten Herleitung der Mathematik der Bézierkurven an.
Regeln
Im obigen Text sind dir vielleicht schon einige "Regeln" für Bézierkurven aufgefallen:
- Der Polynomgrad ist auch der Grad der Kurven.
- Wenn du Krümmungen benötigst, benötigst du mindestens eine Bézierkurve vom Grad .
- Eine Bézierkurve beginnt immer tangential zu der Linie zwischen dem Startpunkt und dem ersten Kontrollpunkt (und endet tangential zu der Linie zwischen dem letzten Kontrollpunkt und dem Endpunkt).
B-Splines
Grundlagen
Dieses Video listet zu Beginn die praktischen Probleme mit Bézierkurven auf. Zum Beispiel, dass das Hinzufügen oder Ändern eines Kontrollpunktes die gesamte Kurve verändert. Diese Probleme können gelöst werden, indem man mehrere Bézierkurven miteinander verbindet. Das Ergebnis ist ein sogenannter Spline, insbesondere ein B-Spline (Basis Spline). Das Video erklärt auch, dass eine Vereinigung von quadratischen Bézierkurven einen uniformen quadratischen B-Spline und eine Vereinigung von kubischen Bézierkurven einen uniformen kubischen B-Spline bildet.
Aus den Videos können wir nützliche "Regeln" für B-Splines entnehmen:
- Der erste und letzte Kontrollpunkt ist der End/Startpunkt des Splines.
- Wie bei Bézierkurven beginnen Splines immer tangential zur Linie zwischen dem Startpunkt und dem ersten Kontrollpunkt (und enden tangential zur Linie zwischen dem letzten Kontrollpunkt und dem Endpunkt).
- Eine Vereinigung von Bézierkurven mit dem Grad hat Kontrollpunkte.
- Da man in den meisten Fällen mit kubischen B-Splines arbeitet, kann man sagen, dass Kontrollpunkte zu Béziersegmenten und diese wiederum zu Segment-Knotenpunkten führen.
- Ein B-Spline mit dem Grad bietet in jedem Punkt eine stetige Ableitung der Ordnung.
- Für einen kubischen B-Spline bedeutet dies, dass sich die Krümmung (Ableitung zweiter Ordnung) nicht ändert, wenn man von einem Segment zum nächsten reist. Dies ist eine sehr nützliche Eigenschaft, wie wir später sehen werden.
Wenn du an weiteren Details über die Eigenschaften von B-Splines interessiert bist, dann schau dir das Video MOOC Curves 8.2: Eigenschaften von B-Spline Kurven an.
Grundlage
Der Name B-Spline steht für Basis Spline. Anstatt den Spline als eine Kombination von Bézierkurven zu bilden, besteht der Ansatz darin, denselben Spline auf eine andere Weise zu modellieren. Die Idee ist hierbei, einen anderen Satz von Polynomen als Basis zu verwenden. Eine Linearkombination dieser Basispolynome mit der Ordnung bildet den B-Spline. Dieses Video erklärt den Übergang von den Bézier Kontrollpunkten zu den polynomialen Basisfunktionen, die den Spline beschreiben. Mathematisch können wir einen B-Spline mit dieser Formel beschreiben:
Dabei ist der -te Kontrollpunkt des B-Splines und zugleich ein Faktor für das -te Basispolynom . Jedes Basispolynom beschreibt den Spline in einem bestimmten Bereich und daher wirkt sich das Verschieben eines Kontrollpunktes nicht auf den gesamten Spline aus. Um dies zu verstehen, empfiehlt es sich, einen Blick auf this video ab Minute 2:23 zu werfen.
Wie im Video erklärt, sind die Basispolynome Bernstein Polynome. Die Menge der Basispolynome für einen bestimmten B-Spline kann auf diese Weise veranschaulicht werden:
Ein Satz von Bernstein Polynomen der Ordnung 4. Sie beschreiben einen B-Spline 4. Ordnung mit 5 Kontrollpunkten.
An jeder Spline Position ist die Summe der Polynome 1 (gekennzeichnet durch die orangefarbene Linie). Am Anfang hat nur das rote Polynom einen Einfluss, da alle anderen Polynome dort 0 sind. Bei größerem wird der Spline durch eine Linearkombination von verschiedenen Basispolynomen beschrieben. In der obigen Abbildung ist jedes Polynom größer als 1 für den gesamten Bereich . Dies ist nicht unbedingt der Fall. Wie im Video gezeigt, sind die Basispolynome grundsätzlich nur für einen bestimmten Bereich der Splineposition größer als 0. Das Intervall, in dem ein Basispolynom größer als 0 ist, wird durch den Knotenvektor beschrieben. Wenn du mehr über den Knotenvektor erfahren möchtest, schau dir dieses Video an.
Nicht-uniforme B-Splines
Eine Eigenschaft der Bernstein Polynome ist, dass bei Betrachtung der verschiedenen S-Spline Bézier Teile die Pfadlänge jedes Teils gleich ist. (Die Pfadlänge wird oft als "Laufzeit" bezeichnet). Wie Sie sich vorstellen können, kann es nützlich sein, B-Splines zu haben, deren Bézier Teile unterschiedliche Pfadlängen haben. Dies kann durch Gewichtung der verschiedenen Polynome erreicht werden:
ist dabei das Gewicht des -ten Kontrollpunktes. Wenn die Gewichte nicht gleich sind, nennt man den B-Spline nicht-uniform.
Vor allem wenn B-Splines für die 3D Modellierung verwendet werden sollen, sind normalisierte, nicht-uniforme B-Splines erforderlich. Die Normalisierung erfolgt durch eine Division durch die gewichteten Basisfunktionen. Wenn also alle gleich sind, erhält man einen einheitlichen B-Spline, unabhängig von der Gewichtung selbst:
Diese nicht-uniformen und rationalen (wegen der Division) B-Splines werden oft NURBS genannt. Ein Blick auf die Formel zeigt, dass es sich tatsächlich um einen B-Spline mit einer gewichteten Basis handelt:
wohingegen
B-splines in FreeCAD
FreeCAD bietet die Möglichkeit, uniforme oder nicht-uniforme B-Splines beliebigen Grades in 2D über die Skizzierer Arbeitsbereich zu erstellen.
Erstellung
Um B-Splines zu erstellen, gehe in eine Skizze und verwende die Werkzeugleistenschaltfläche B-spline erstellen. Dann Linksklick um einen Kontrollpunkt zu setzen, bewege die Maus Linksklick, um den nächsten Kontrollpunkt zu setzen und so weiter. Abschließend Rechtsklick, um die Definition abzuschließen und den B-Spline zu erstellen.
Standardmäßig werden gleichmäßige kubische Splines erstellt, es sei denn, es gibt nicht genügend Kontrollpunkte, um dies zu tun. Wenn du also einen B-Spline mit nur 2 Kontrollpunkten erstellst, erhältst du natürlich einen Spline, der eine einzelne lineare Bézierkurve ist, für 3 Kontrollpunkte erhältst du eine quadratische Bézierkurve, erst mit 5 Kontrollpunkten erhältst du einen kubischen B-Spline, der aus 2 Béziersegmenten besteht.
Um periodische B-Splines (B-Splines, die eine geschlossene Kurve bilden) zu erstellen, verwende die Werkzeugleistenschaltfläche Periodische B-spline. Es ist nicht notwendig, den letzten Kontrollpunkt auf den ersten zu setzen, da der B-Spline automatisch geschlossen wird:
B-Splines können auch aus bestehenden Skizzen Segmenten erzeugt werden. Markiere dazu die Elemente und drücke den Werkzeugleistenknopfltfläche Geometrie in B-Spline umwandeln.
Ändern des Grads
Um den Grad zu ändern, wähle den B-Spline und verwende entweder die Werkzeugleistenschaltfläche B-Spline-Grad erhöhen oder
B-Spline-Grad vermindern.
Hinweis: Das Verringern des Grads kann eine vorherige Erhöhung des Grads nicht rückgängig machen, siehe die Wiki Seite B-spline Grad vermindern für eine Erklärung.
Ändern der Knotenvielfalt
Die Punkte, an denen zwei Bézierkurven miteinander verbunden werden, um den B-Spline zu bilden, werden Knoten genannt. Die Knotenmultiplikation bestimmt, wie die Bézier Teile verbunden werden, siehe die Wiki Seite Knotenvielfalt erhöhen für Details.
Um die Knotenvielfalt zu ändern, verwende die Werkzeugleistenschaltflächen in der B-spline Knotenvielfalt erhöhen oder
B-spline Knotenvielfalt vermindern.
Hinweis: Das Erstellen von zwei B-Splines, die miteinander verbunden sind, wird sich nicht zu einem einzigen neuen B-Spline vereinigen. Ihr Verbindungspunkt ist also kein Knoten. Die einzige Möglichkeit, einen neuen Knoten in einem bestehenden B-Spline zu erhalten, besteht darin, den Grad zu verringern. Dabei können jedoch viele neue Knoten entstehen. Daher ist es besser, den B-Spline mit mehr Kontrollpunkten neu zu zeichnen.
Ändern des Gewichts
Um jeden Kontrollpunkt herum siehst du einen dunkelgelben Kreis. Sein Radius legt das Gewicht für den entsprechenden Kontrollpunkt fest. Standardmäßig haben alle Kreise den Radius 1. Dies wird durch eine Radiusbeschränkung für den ersten Kontrollpunktkreis angezeigt.
Um einen nicht-uniformen B-Spline zu erzeugen, müssen die Gewichte ungleichmäßig sein. Um dies zu erreichen, kannst du entweder die Radiusbeschränkung des ersten Kontrollpunktkreises ändern:
File:Sketcher Changing-control-point-weigth-constraint.gif
oder du löschst die Beschränkung, dass alle Kreise gleich sind, und legst dann verschiedene Radiusbeschränkungen für die Kreise fest.
Wenn keine Radiusbeschränkung festgelegt ist, kannst du den Radius auch durch Ziehen ändern:
Am Beispiel des Ziehens siehst du, dass ein hohes Gewicht die Kurve zum Kontrollpunkt zieht, während ein sehr niedriges Gewicht die Kurve so verändert, als ob der Kontrollpunkt fast nicht existiert.
Wenn du dir die Erstellungsfunktion für nicht-uniformee rationale B-Splines ansehst, siehst du, dass ein Gewicht von Null zu einer Division durch Null führen würde. Daher kannst du nur Gewichte größer als Null angeben.
Informationen anzeigen
Da die Form eines B-Splines nicht viel über seine Eigenschaften aussagt, bietet FreeCAD verschiedene Werkzeuge, um die Eigenschaften anzuzeigen:
| Eigenschaft | Werkzeugleistenschaltfläche |
| Grad | |
| Kontrollpolygon | |
| Krümmungskamm | |
| Knotenvielfalt | |
| Gewichte |
Begrenzungen
Im Augenblick (FreeCAD 0.19) gibt es einige Begrenzungen bei der Verwendung von Splines, die du kennen solltest:
- Du kannst keine tangentialen Beschränkungen festlegen.
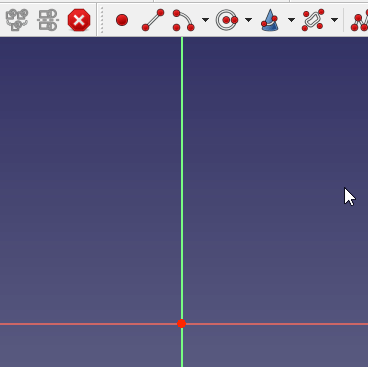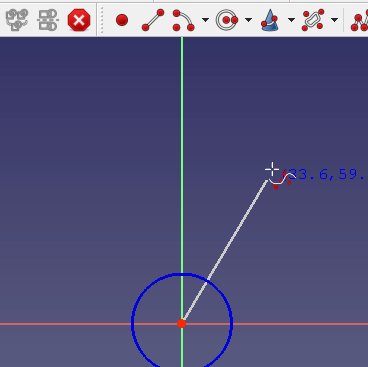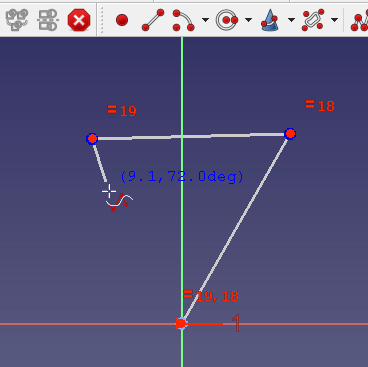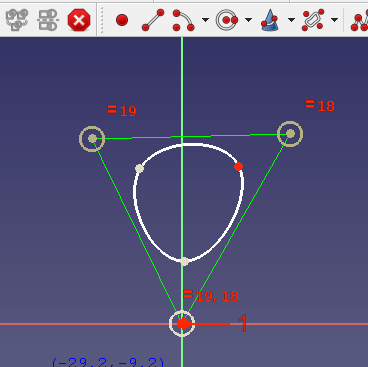
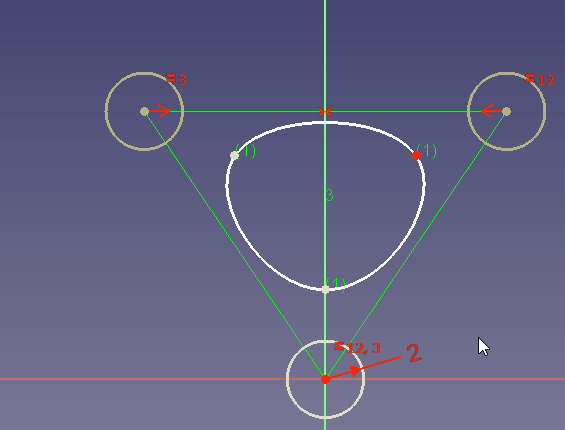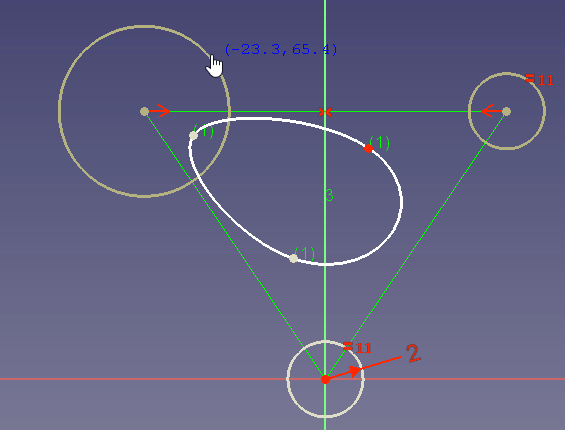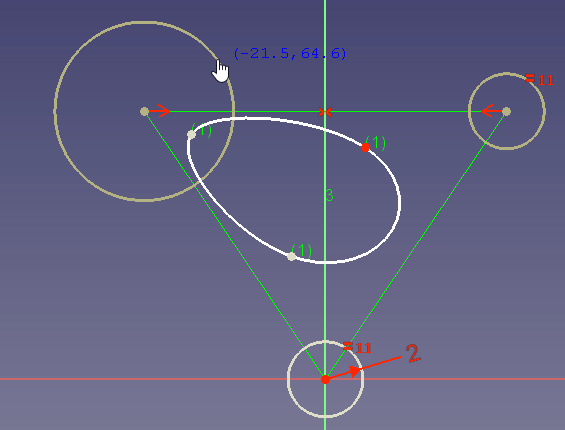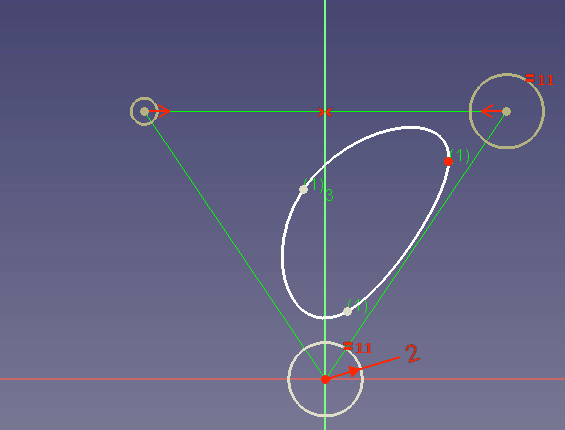
In diesem Beispiel
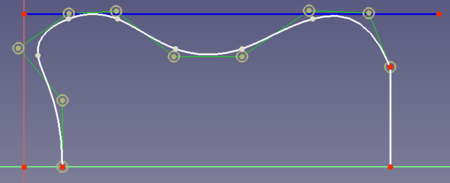
willst du sicherstellen, dass der Spline die blaue Kurve 2 mal tangential berührt. Dies ist sinnvoll, da die blaue Linie z.B. die räumliche Grenze für deinen Entwurf sein könnte. - Du kannst keinen neuen Kontrollpunkt zwischen zwei ausgewählten bestehenden Kontrollpunkten einfügen. Es gibt keine andere Möglichkeit, als den Spline neu zu zeichnen.
- Du kannst einen Kontrollpunkt nicht löschen. Auch in diesem Fall musst du den Spline neu zeichnen.
- Du kannst keine Versatzkurve für einen B-Spline mit dem Werkzeug Entwurf Versatz erstellen.
Typische Anwendungsfälle
Entsprechend den Eigenschaften von B-Splines gibt es 3 Hauptanwendungsfälle:
- Kurven, die tangential zu einer bestimmten Richtung beginnen/enden. Ein Beispiel hierfür ist das Motivationsbeispiel oben.
- Kurven, die größere Entwürfe beschreiben und die Freiheit lokaler Änderungen bieten. Siehe dieses Beispiel unten.
- Kurven, die eine gewisse Stetigkeit (Ableitung) bieten. Siehe dieses Beispiel unten.
Gestaltung
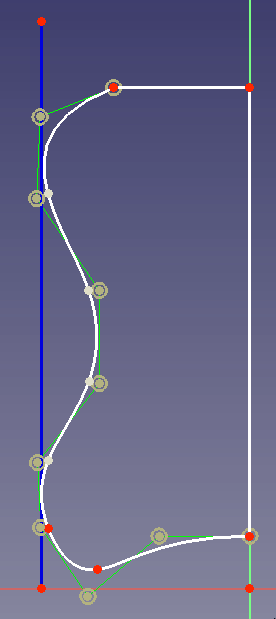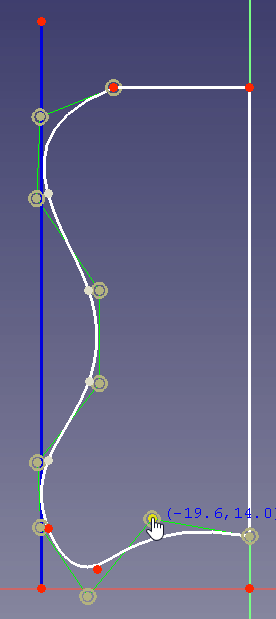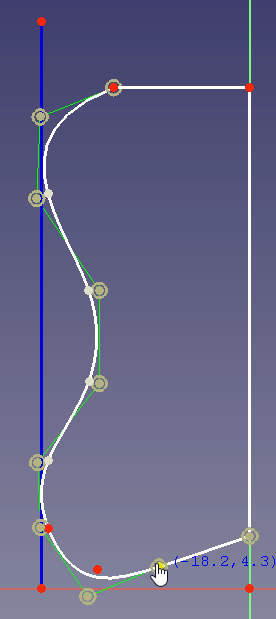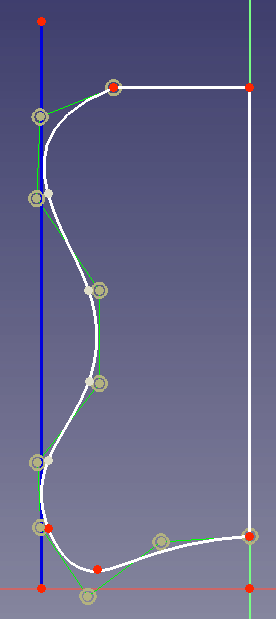
Take for example the case that you design a housing of a kitchen mixer. Its desired shape should look like this one:
To define the outer form it is advantageous to use a B-spline because when you change a control point to change the curvature at the bottom, the curvature at the side and top will not be changed:
Stetigkeit an geometrischen Übergängen
There are several cases where it is physically necessary to have a certain surface continuity at geometric transitions. Take for example the inner walls of a fluid channel. When you have a change in the diameter of the channel, you don't want to have an edge because edges would introduce turbulences. Therefore, like in the motivation example above, one uses splines for this purpose.
The development of the Bézier curves was initially triggered by the French car industry. Besides the saving of material and the reduction of the air flow drag, the look of the cars should also be improved. And when you look at the fancy design of French cars from the 60's and 70's you see that the Bézier curves gave car design a boost.
Let's take for example this task in the design of cars: The car fender should "look nice". Here is a basic sketch of our task:
"Looking nice" means that the (potential) customer looks at the fender and does not see unexpected light reflections and also no sudden changes in the reflection from the automotive paint at all. So what do you need to avoid changes in the reflections? Looking closely to the fender:
At the spatial area above the edge the intensity of reflected light is low (denoted by the red ellipse) because no light is directly reflected in the direction from the edge to the eye.
you see when there is an edge, there is a spatial area where the reflected light has less intensity and this is what you will notice when looking at the fender. To avoid this you need a continuous change in the slope of your surface elements. The slope is the first order derivative and as explained in section Basics, a second degree (quadratic) B-spline offers at every point a continuous first order derivative.
But is this really sufficient? At the point of geometric transition we have now at both sides the same slope, but the slope might change differently at both sides. Then we have this situation:
So we have also spatial areas in which the intensity of reflected light is different. To avoid this, we need at the geometrical point of transition also a continuity of the second order derivative and thus a cubic B-spline.