Topological data scripting/pl: Difference between revisions
(Updating to match new version of source page) |
No edit summary |
||
| (223 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
<languages/> |
|||
This page describes several methods for creating and modifying [[Part Module|Part shapes]] from python. Before reading this page, if you are new to python, it is a good idea to read about [[Introduction to Python|python scripting]] and [[FreeCAD Scripting Basics|how python scripting works in FreeCAD]]. |
|||
{{Docnav/pl |
|||
== Introduction == |
|||
|[[FreeCAD_Scripting_Basics/pl|Podstawy tworzenia skryptów FreeCAD]] |
|||
We will here explain you how to control the [[Part Module]] directly from the FreeCAD python interpreter, or from any external script. The basics about Topological data scripting are described in [[Part_Module#Explaining_the_concepts|Part Module Explaining the concepts]]. Be sure to browse the [[Scripting]] section and the [[FreeCAD Scripting Basics]] pages if you need more information about how python scripting works in FreeCAD. |
|||
|[[Mesh_Scripting/pl|Skrytpy w Środowisku Siatek]] |
|||
}} |
|||
{{TOCright}} |
|||
=== Class Diagram === |
|||
This is a [http://en.wikipedia.org/wiki/Unified_Modeling_Language Unified Modeling Language (UML)] overview of the most important classes of the Part module: |
|||
[[Image:Part_Classes.jpg|center|Python classes of the Part module]] |
|||
<span id="Introduction"></span> |
|||
=== Geometry === |
|||
==Wprowadzenie== |
|||
The geometric objects are the building block of all topological objects: |
|||
* '''Geom''' Base class of the geometric objects |
|||
* '''Line''' A straight line in 3D, defined by starting point and end point |
|||
* '''Circle''' Circle or circle segment defined by a center point and start and end point |
|||
* '''......''' And soon some more |
|||
Tutaj wyjaśnimy Ci jak kontrolować środowisko [[Part_Workbench/pl|Część]] bezpośrednio z interpretera FreeCAD Python, lub z dowolnego zewnętrznego skryptu. Przejrzyj sekcję [[Power_users_hub/pl| o skryptach]] oraz strony [[FreeCAD_Scripting_Basics/pl|Podstawy tworzenia skryptów FreeCAD]], jeśli potrzebujesz więcej informacji na temat działania skryptów Pythona w FreeCAD. Jeśli jesteś początkującym użytkownikiem środowiska Python, dobrze jest najpierw przeczytać [[Introduction_to_Python/pl|Wprowadzenie do środowiska Python]]. |
|||
=== Topology === |
|||
The following topological data types are available: |
|||
* '''Compound''' A group of any type of topological object. |
|||
* '''Compsolid''' A composite solid is a set of solids connected by their faces. It expands the notions of WIRE and SHELL to solids. |
|||
* '''Solid''' A part of space limited by shells. It is three dimensional. |
|||
* '''Shell''' A set of faces connected by their edges. A shell can be open or closed. |
|||
* '''Face''' In 2D it is part of a plane; in 3D it is part of a surface. Its geometry is constrained (trimmed) by contours. It is two dimensional. |
|||
* '''Wire''' A set of edges connected by their vertices. It can be an open or closed contour depending on whether the edges are linked or not. |
|||
* '''Edge''' A topological element corresponding to a restrained curve. An edge is generally limited by vertices. It has one dimension. |
|||
* '''Vertex''' A topological element corresponding to a point. It has zero dimension. |
|||
* '''Shape''' A generic term covering all of the above. |
|||
<span id="See_also"></span> |
|||
=== Quick example : Creating simple topology === |
|||
==Zobacz również== |
|||
* [[Part_scripting/pl|Skrypty w środowisku Część]] |
|||
[[Image:Wire.png|right|Wire]] |
|||
* [[OpenCASCADE/pl|OpenCASCADE]] |
|||
<span id="Class_diagram"></span> |
|||
We will now create a topology by constructing it out of simpler geometry. |
|||
==Schemat klas== |
|||
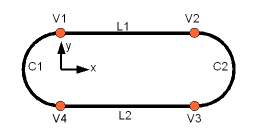
As a case study we use a part as seen in the picture which consists of |
|||
four vertexes, two circles and two lines. |
|||
To jest [http://en.wikipedia.org/wiki/Unified_Modeling_Language Unified Modeling Language ''(UML)''] przegląd najważniejszych klas modułu Część: |
|||
==== Creating Geometry ==== |
|||
[[Image:Part_Classes.jpg|klasy Python, modułu Część]] |
|||
First we have to create the distinct geometric parts of this wire. |
|||
{{Top}} |
|||
And we have to take care that the vertexes of the geometric parts |
|||
<span id="Geometry"></span> |
|||
are at the '''same''' position. Otherwise later on we might not be |
|||
===Geometria=== |
|||
able to connect the geometric parts to a topology! |
|||
Obiekty geometryczne są elementami składowymi wszystkich obiektów topologicznych: |
|||
So we create first the points: |
|||
* '''Geom''' Klasa bazowa obiektów geometrycznych. |
|||
<syntaxhighlight> |
|||
* '''Linia''' Linia prosta w przestrzeni 3D, zdefiniowana przez punkt początkowy i punkt końcowy. |
|||
from FreeCAD import Base |
|||
* '''Okrąg''' Okrąg lub odcinek okręgu zdefiniowany przez punkt środkowy oraz punkt początkowy i końcowy. |
|||
V1 = Base.Vector(0,10,0) |
|||
* I tak dalej. |
|||
V2 = Base.Vector(30,10,0) |
|||
{{Top}} |
|||
V3 = Base.Vector(30,-10,0) |
|||
<span id="Topology"></span> |
|||
V4 = Base.Vector(0,-10,0) |
|||
===Topologia=== |
|||
</syntaxhighlight> |
|||
==== Arc ==== |
|||
Dostępne są następujące typy danych topologicznych: |
|||
[[Image:Circel.png|right|Circle]] |
|||
* '''Złożenie''' Grupa obiektów topologicznych dowolnego typu. |
|||
* '''Bryła złożona''' Bryła złożona to zbiór brył połączonych ścianami. Rozszerza pojęcia WIRE i SHELL na bryły. |
|||
* '''Bryła''' Część przestrzeni ograniczona powłokami. Jest trójwymiarowa. |
|||
* '''Powłoka''' Zbiór ścian połączonych krawędziami. Powłoka może być otwarta lub zamknięta. |
|||
* '''Ścina''' W 2D jest częścią płaszczyzny, w 3D jest częścią powierzchni. Jego geometria jest ograniczona ''(przycięta)'' przez kontury. Jest dwuwymiarowa. |
|||
* '''Linia łamana''' ''(polilinia)'' Zbiór krawędzi połączonych wierzchołkami. Może to być kontur otwarty lub zamknięty, w zależności od tego, czy krawędzie są połączone, czy nie. |
|||
* '''Krawędź''' Element topologiczny odpowiadający krzywej ograniczonej. Krawędź jest na ogół ograniczona wierzchołkami. Ma jeden wymiar. |
|||
* '''Wierzchołek''' Element topologiczny odpowiadający punktowi. Ma zero wymiarów. |
|||
* '''Kształt''' Termin ogólny obejmujący wszystkie powyższe. |
|||
{{Top}} |
|||
<span id="Example:_Create_simple_topology"></span> |
|||
==Przykład: Utwórz prostą topologię== |
|||
[[Image:Wire.png|Linia łamana]] |
|||
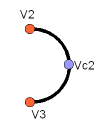
To create an arc of circle we make a helper point and create the arc of |
|||
circle through three points: |
|||
<syntaxhighlight> |
|||
VC1 = Base.Vector(-10,0,0) |
|||
C1 = Part.Arc(V1,VC1,V4) |
|||
# and the second one |
|||
VC2 = Base.Vector(40,0,0) |
|||
C2 = Part.Arc(V2,VC2,V3) |
|||
</syntaxhighlight> |
|||
==== Line ==== |
|||
Stworzymy teraz topologię poprzez skonstruowanie jej z prostszej geometrii. Jako studium przypadku użyjemy części widocznej na rysunku, która składa się z czterech wierzchołków, dwóch łuków i dwóch linii. |
|||
[[Image:Line.png|right|Line]] |
|||
{{Top}} |
|||
<span id="Create_geometry"></span> |
|||
===Tworzenie geometrii=== |
|||
Najpierw tworzymy odrębne części geometryczne tej linii łamanej. Upewniamy się, że części, które mają być później połączone, mają wspólne wierzchołki. |
|||
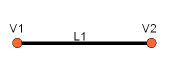
The line can be created very simple out of the points: |
|||
<syntaxhighlight> |
|||
Więc najpierw tworzymy punkty: |
|||
L1 = Part.Line(V1,V2) |
|||
# and the second one |
|||
{{Code|code= |
|||
L2 = Part.Line(V4,V3) |
|||
import FreeCAD as App |
|||
</syntaxhighlight> |
|||
import Part |
|||
==== Putting all together ==== |
|||
V1 = App.Vector(0, 10, 0) |
|||
The last step is to put the geometric base elements together |
|||
V2 = App.Vector(30, 10, 0) |
|||
and bake a topological shape: |
|||
V3 = App.Vector(30, -10, 0) |
|||
<syntaxhighlight> |
|||
V4 = App.Vector(0, -10, 0) |
|||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Make a prism ==== |
|||
<span id="Arc"></span> |
|||
Now extrude the wire in a direction and make an actual 3D shape: |
|||
===Łuk=== |
|||
<syntaxhighlight> |
|||
[[Image:Circel.png|Okrąg]] |
|||
Dla każdego łuku potrzebujemy punktu pomocniczego: |
|||
{{Code|code= |
|||
VC1 = App.Vector(-10, 0, 0) |
|||
C1 = Part.Arc(V1, VC1, V4) |
|||
VC2 = App.Vector(40, 0, 0) |
|||
C2 = Part.Arc(V2, VC2, V3) |
|||
}} |
|||
{{Top}} |
|||
<span id="Line"></span> |
|||
===Linia=== |
|||
[[Image:Line.png|Linia]] |
|||
Odcinki linii można utworzyć z dwóch punktów: |
|||
{{Code|code= |
|||
L1 = Part.LineSegment(V1, V2) |
|||
L2 = Part.LineSegment(V3, V4) |
|||
}} |
|||
{{Top}} |
|||
<span id="Put_it_all_together"></span> |
|||
===Połącz wszystko w całość=== |
|||
Ostatnim krokiem jest zestawienie geometrycznych elementów bazowych razem i uzyskanie kształtu topologicznego: |
|||
{{Code|code= |
|||
S1 = Part.Shape([C1, L1, C2, L2]) |
|||
}} |
|||
{{Top}} |
|||
<span id="Make_a_prism"></span> |
|||
===Utwórz graniastosłup=== |
|||
Teraz wyciągnij linę łamaną w odpowiednim kierunku i stwórz rzeczywisty kształt 3D: |
|||
{{Code|code= |
|||
W = Part.Wire(S1.Edges) |
W = Part.Wire(S1.Edges) |
||
P = W.extrude( |
P = W.extrude(App.Vector(0, 0, 10)) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Show it all ==== |
|||
<span id="Show_it_all"></span> |
|||
<syntaxhighlight> |
|||
===Pokaż to wszystko=== |
|||
{{Code|code= |
|||
Part.show(P) |
Part.show(P) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
== Creating basic shapes == |
|||
<span id="Create_basic_shapes"></span> |
|||
You can easily create basic topological objects with the "make...()" |
|||
==Utwórz podstawowe kształty== |
|||
methods from the Part Module: |
|||
<syntaxhighlight> |
|||
Możesz łatwo tworzyć podstawowe obiekty topologiczne za pomocą metod {{incode|make...()}} z modułu Część: |
|||
b = Part.makeBox(100,100,100) |
|||
{{Code|code= |
|||
b = Part.makeBox(100, 100, 100) |
|||
Part.show(b) |
Part.show(b) |
||
}} |
|||
</syntaxhighlight> |
|||
A couple of other make...() methods available: |
|||
Niektóre dostępne metody {{incode|make...()}}: |
|||
* '''makeBox(l,w,h)''': Makes a box located in p and pointing into the direction d with the dimensions (l,w,h) |
|||
* {{incode|makeBox(l, w, h, [p, d])}} Tworzy sześcian znajdujący się w punkcie p i skierowany w kierunku d o wymiarach ''(l,w,h)''. |
|||
* '''makeCircle(radius)''': Makes a circle with a given radius |
|||
* {{incode|makeCircle(radius)}} Tworzy okrąg o zadanym promieniu. |
|||
* '''makeCone(radius1,radius2,height)''': Makes a cone with a given radii and height |
|||
* {{incode|makeCone(radius1, radius2, height)}}. Tworzy stożek o podanych promieniach i wysokościach. |
|||
* '''makeCylinder(radius,height)''': Makes a cylinder with a given radius and height. |
|||
* {{incode|makeCylinder(radius, height)}}. Tworzy walec o zadanym promieniu i wysokości. |
|||
* '''makeLine((x1,y1,z1),(x2,y2,z2))''': Makes a line of two points |
|||
* {{incode|makeLine((x1, y1, z1), (x2, y2, z2))}} Tworzy prostą z dwóch punktów. |
|||
* '''makePlane(length,width)''': Makes a plane with length and width |
|||
* {{incode|makePlane(length, width)}} Tworzy płaszczyznę o określonej długości i szerokości. |
|||
* '''makePolygon(list)''': Makes a polygon of a list of points |
|||
* {{incode|makePolygon(list)}} {{incode|makePolygon(list)}} Tworzy wielokąt z listy punktów. |
|||
* '''makeSphere(radius)''': Make a sphere with a given radius |
|||
* {{incode|makeSphere(radius)}} Tworzy sferę o zadanym promieniu. |
|||
* '''makeTorus(radius1,radius2)''': Makes a torus with a given radii |
|||
* {{incode|makeTorus(radius1, radius2)}} Tworzy torus o podanych promieniach. |
|||
See the [[Part API]] page for a complete list of available methods of the Part module. |
|||
Zobacz stronę [[Part_API/pl|skrypty środowiska Część]] lub [https://freecad-python-stubs.readthedocs.io/en/latest/autoapi/Part/ dokumentacja API środowiska Część generowana automatycznie] aby zobaczyć pełną listę dostępnych metod modułu Część. |
|||
{{Top}} |
|||
<span id="Import_modules"></span> |
|||
==Import modułów== |
|||
Najpierw musimy zaimportować moduły FreeCAD i Część, aby móc korzystać z ich zawartości w Pythonie: |
|||
{{Code|code= |
|||
==== Importing the needed modules ==== |
|||
import FreeCAD as App |
|||
First we need to import the Part module so we can use its contents in python. |
|||
We'll also import the Base module from inside the FreeCAD module: |
|||
<syntaxhighlight> |
|||
import Part |
import Part |
||
}} |
|||
from FreeCAD import Base |
|||
{{Top}} |
|||
</syntaxhighlight> |
|||
<span id="Create_a_vector"></span> |
|||
==== Creating a Vector ==== |
|||
===Utwórz wektor=== |
|||
[http://en.wikipedia.org/wiki/Euclidean_vector Vectors] are one of the most |
|||
important pieces of information when building shapes. They contain a 3 numbers |
|||
[http://en.wikipedia.org/wiki/Euclidean_vector Wektory] są jedną z najważniejszych informacji przy tworzeniu kształtów. Zazwyczaj zawierają trzy liczby ''(ale niekoniecznie zawsze)'': współrzędne kartezjańskie X, Y i Z. Tworzysz wektor w ten sposób: |
|||
usually (but not necessarily always) the x, y and z cartesian coordinates. You |
|||
create a vector like this: |
|||
{{Code|code= |
|||
<syntaxhighlight> |
|||
myVector = |
myVector = App.Vector(3, 2, 0) |
||
}} |
|||
</syntaxhighlight> |
|||
We just created a vector at coordinates x=3, y=2, z=0. In the Part module, |
|||
Właśnie utworzyliśmy wektor o współrzędnych X = 3, Y = 2, Z = 0. W module Part, wektory są używane wszędzie. Kształty części używają również innego rodzaju reprezentacji punktów zwanej Vertex, która jest po prostu kontenerem dla wektora. Dostęp do wektora wierzchołka uzyskujesz w następujący sposób: |
|||
vectors are used everywhere. Part shapes also use another kind of point |
|||
representation, called Vertex, which is acually nothing else than a container |
|||
{{Code|code= |
|||
for a vector. You access the vector of a vertex like this: |
|||
<syntaxhighlight> |
|||
myVertex = myShape.Vertexes[0] |
myVertex = myShape.Vertexes[0] |
||
print |
print(myVertex.Point) |
||
> Vector (3, 2, 0) |
> Vector (3, 2, 0) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Creating an Edge ==== |
|||
<span id="Create_an_edge"></span> |
|||
An edge is nothing but a line with two vertexes: |
|||
===Utwórz krawędź=== |
|||
<syntaxhighlight> |
|||
edge = Part.makeLine((0,0,0), (10,0,0)) |
|||
Krawędź to nic innego jak linia z dwoma wierzchołkami: |
|||
{{Code|code= |
|||
edge = Part.makeLine((0, 0, 0), (10, 0, 0)) |
|||
edge.Vertexes |
edge.Vertexes |
||
> [<Vertex object at 01877430>, <Vertex object at 014888E0>] |
> [<Vertex object at 01877430>, <Vertex object at 014888E0>] |
||
}} |
|||
</syntaxhighlight> |
|||
Note: You can also create an edge by passing two vectors: |
|||
Uwaga: Możesz również utworzyć krawędź poprzez przekazanie dwóch wektorów: |
|||
<syntaxhighlight> |
|||
vec1 = Base.Vector(0,0,0) |
|||
{{Code|code= |
|||
vec2 = Base.Vector(10,0,0) |
|||
vec1 = App.Vector(0, 0, 0) |
|||
vec2 = App.Vector(10, 0, 0) |
|||
line = Part.LineSegment(vec1, vec2) |
|||
edge = line.toShape() |
edge = line.toShape() |
||
}} |
|||
</syntaxhighlight> |
|||
You can find the length and center of an edge like this: |
|||
Możesz znaleźć długość i środek krawędzi w ten sposób: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
edge.Length |
edge.Length |
||
> 10.0 |
> 10.0 |
||
edge.CenterOfMass |
edge.CenterOfMass |
||
> Vector (5, 0, 0) |
> Vector (5, 0, 0) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Putting the shape on screen ==== |
|||
<span id="Put_the_shape_on_screen"></span> |
|||
So far we created an edge object, but it doesn't appear anywhere on screen. |
|||
===Wyświetl kształt na ekranie=== |
|||
This is because we just manipulated python objects here. The FreeCAD 3D scene |
|||
only displays what you tell it to display. To do that, we use this simple |
|||
Do tej pory utworzyliśmy obiekt krawędziowy, ale nie pojawia się on nigdzie na ekranie. Dzieje się tak dlatego, że scena 3D FreeCAD wyświetla tylko to, co każesz jej wyświetlić. Aby to zrobić, użyjemy prostej metody: |
|||
method: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
Part.show(edge) |
Part.show(edge) |
||
}} |
|||
</syntaxhighlight> |
|||
An object will be created in our FreeCAD document, and our "edge" shape |
|||
will be attributed to it. Use this whenever it's time to display your |
|||
creation on screen. |
|||
Funkcja show tworzy obiekt w naszym dokumencie FreeCAD i przypisuje mu nasz kształt "krawędzi". Używaj jej zawsze wtedy, gdy chcesz wyświetlić swoje dzieło na ekranie. |
|||
==== Creating a Wire ==== |
|||
{{Top}} |
|||
A wire is a multi-edge line and can be created from a list of edges |
|||
<span id="Create_a_wire"></span> |
|||
or even a list of wires: |
|||
===Utwórz linie łamaną=== |
|||
<syntaxhighlight> |
|||
edge1 = Part.makeLine((0,0,0), (10,0,0)) |
|||
Linia łamana jest linią o wielu krawędziach i może być utworzona z listy krawędzi lub nawet z listy linii łamanych: |
|||
edge2 = Part.makeLine((10,0,0), (10,10,0)) |
|||
wire1 = Part.Wire([edge1,edge2]) |
|||
{{Code|code= |
|||
edge3 = Part.makeLine((10,10,0), (0,10,0)) |
|||
edge1 = Part.makeLine((0, 0, 0), (10, 0, 0)) |
|||
edge2 = Part.makeLine((10, 0, 0), (10, 10, 0)) |
|||
wire1 = Part.Wire([edge1, edge2]) |
|||
edge3 = Part.makeLine((10, 10, 0), (0, 10, 0)) |
|||
edge4 = Part.makeLine((0, 10, 0), (0, 0, 0)) |
|||
wire2 = Part.Wire([edge3, edge4]) |
|||
wire3 = Part.Wire([wire1, wire2]) |
|||
wire3.Edges |
wire3.Edges |
||
> [<Edge object at 016695F8>, <Edge object at 0197AED8>, <Edge object at 01828B20>, <Edge object at 0190A788>] |
> [<Edge object at 016695F8>, <Edge object at 0197AED8>, <Edge object at 01828B20>, <Edge object at 0190A788>] |
||
Part.show(wire3) |
Part.show(wire3) |
||
}} |
|||
</syntaxhighlight> |
|||
Part.show(wire3) will display the 4 edges that compose our wire. Other |
|||
{{incode|Part.show(wire3)}} wyświetli 4 krawędzie, z których składa się nasza linia łamana. Inne przydatne informacje mogą być łatwo pobrane: |
|||
useful information can be easily retrieved: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
wire3.Length |
wire3.Length |
||
> 40.0 |
> 40.0 |
||
| Line 190: | Line 243: | ||
wire2.isClosed() |
wire2.isClosed() |
||
> False |
> False |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Creating a Face ==== |
|||
<span id="Create_a_face"></span> |
|||
Only faces created from closed wires will be valid. In this example, wire3 |
|||
===Utwórz ścianę=== |
|||
is a closed wire but wire2 is not a closed wire (see above) |
|||
<syntaxhighlight> |
|||
Tylko ściany utworzone z linii łamanych będą poprawne. W tym przykładzie linia łamana3 jest zamknięta, ale linia łamana2 nie jest ''(patrz wyżej)'': |
|||
{{Code|code= |
|||
face = Part.Face(wire3) |
face = Part.Face(wire3) |
||
face.Area |
face.Area |
||
> 99. |
> 99.99999999999999 |
||
face.CenterOfMass |
face.CenterOfMass |
||
> Vector (5, 5, 0) |
> Vector (5, 5, 0) |
||
| Line 205: | Line 261: | ||
> True |
> True |
||
sface = Part.Face(wire2) |
sface = Part.Face(wire2) |
||
sface.isValid() |
|||
> False |
> False |
||
}} |
|||
</syntaxhighlight> |
|||
Only faces will have an area, not wires nor edges. |
|||
Tylko twarze będą posiadać obszar, linie łamane i krawędzie nie. |
|||
==== Creating a Circle ==== |
|||
{{Top}} |
|||
A circle can be created as simply as this: |
|||
<span id="Create_a_circle"></span> |
|||
<syntaxhighlight> |
|||
===Utwórz okrąg=== |
|||
Okrąg może być utworzony w ten sposób: |
|||
{{Code|code= |
|||
circle = Part.makeCircle(10) |
circle = Part.makeCircle(10) |
||
circle.Curve |
circle.Curve |
||
> Circle (Radius : 10, Position : (0, 0, 0), Direction : (0, 0, 1)) |
> Circle (Radius : 10, Position : (0, 0, 0), Direction : (0, 0, 1)) |
||
}} |
|||
</syntaxhighlight> |
|||
If you want to create it at certain position and with certain direction: |
|||
Jeśli chcesz utworzyć go w określonej pozycji i z określonym kierunkiem: |
|||
<syntaxhighlight> |
|||
ccircle = Part.makeCircle(10, Base.Vector(10,0,0), Base.Vector(1,0,0)) |
|||
{{Code|code= |
|||
ccircle = Part.makeCircle(10, App.Vector(10, 0, 0), App.Vector(1, 0, 0)) |
|||
ccircle.Curve |
ccircle.Curve |
||
> Circle (Radius : 10, Position : (10, 0, 0), Direction : (1, 0, 0)) |
> Circle (Radius : 10, Position : (10, 0, 0), Direction : (1, 0, 0)) |
||
}} |
|||
</syntaxhighlight> |
|||
ccircle will be created at distance 10 from origin on x and will be facing |
|||
okrąg zostanie utworzony w odległości 10 od początku X i będzie skierowany na zewnątrz wzdłuż osi X. Uwaga: {{incode|makeCircle()}} akceptuje tylko {{incode|App.Vector()}} dla parametrów position i parametry jako wektory normalne, a nie krotki. Możesz również utworzyć część okręgu przez podanie kąta początkowego i końcowego: |
|||
towards x axis. Note: makeCircle only accepts Base.Vector() for position |
|||
and normal but not tuples. You can also create part of the circle by giving |
|||
{{Code|code= |
|||
start angle and end angle as: |
|||
<syntaxhighlight> |
|||
from math import pi |
from math import pi |
||
arc1 = Part.makeCircle(10, |
arc1 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180) |
||
arc2 = Part.makeCircle(10, |
arc2 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 180, 360) |
||
}} |
|||
</syntaxhighlight> |
|||
Both arc1 and arc2 jointly will make a circle. Angles should be provided in |
|||
Kąty powinny być podane w stopniach. Jeśli masz radiany, po prostu przekonwertuj je za pomocą wzoru: |
|||
degrees, if you have radians simply convert them using formula: |
|||
degrees = radians * 180/ |
{{incode|degrees <nowiki>=</nowiki> radians * 180/pi}} lub za pomocą modułu {{incode|math}} Pythona: |
||
math, of course): |
|||
{{Code|code= |
|||
<syntaxhighlight> |
|||
import math |
|||
degrees = math.degrees(radians) |
degrees = math.degrees(radians) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Creating an Arc along points ==== |
|||
<span id="Create_an_arc_along_points"></span> |
|||
Unfortunately there is no makeArc function but we have Part.Arc function to |
|||
===Utwórz łuk wzdłuż punktów=== |
|||
create an arc along three points. Basically it can be supposed as an arc |
|||
joining start point and end point along the middle point. Part.Arc creates |
|||
Niestety nie ma funkcji {{incode|makeArc()}}, ale mamy funkcję {{incode|Part.Arc()}} do tworzenia łuku przez trzy punkty. Tworzy ona obiekt łuku łączący punkt początkowy z punktem końcowym przez punkt środkowy. Funkcja {{incode|toShape()}} obiektu arc musi zostać wywołana, aby otrzymać obiekt krawędzi, tak samo jak w przypadku użycia {{incode|Part.LineSegment}} zamiast {{incode|Part.makeLine}}. |
|||
an arc object on which .toShape() has to be called to get the edge object, |
|||
the same way as when using Part.Line instead of Part.makeLine. |
|||
{{Code|code= |
|||
<syntaxhighlight> |
|||
arc = Part.Arc( |
arc = Part.Arc(App.Vector(0, 0, 0), App.Vector(0, 5, 0), App.Vector(5, 5, 0)) |
||
arc |
arc |
||
> <Arc object> |
> <Arc object> |
||
arc_edge = arc.toShape() |
arc_edge = arc.toShape() |
||
Part.show(arc_edge) |
|||
</syntaxhighlight> |
|||
}} |
|||
Arc only accepts Base.Vector() for points but not tuples. arc_edge is what |
|||
we want which we can display using Part.show(arc_edge). You can also obtain |
|||
Funkcja {{incode|Arc()}} akceptuje tylko {{incode|App.Vector()}} dla punktów, a nie dla krotek. Możesz również uzyskać łuk używając części okręgu: |
|||
an arc by using a portion of a circle: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
from math import pi |
from math import pi |
||
circle = Part.Circle( |
circle = Part.Circle(App.Vector(0, 0, 0), App.Vector(0, 0, 1), 10) |
||
arc = Part.Arc( |
arc = Part.Arc(circle,0,pi) |
||
}} |
|||
</syntaxhighlight> |
|||
Arcs are valid edges, like lines. So they can be used in wires too. |
|||
Łuki są poprawnymi krawędziami, tak jak linie, więc mogą być również używane w poliliniach. |
|||
{{Top}} |
|||
<span id="Create_a_polygon"></span> |
|||
===Utwórz wielokąt=== |
|||
Wielokąt jest po prostu polilinią o wielu prostych krawędziach. Funkcja {{incode|makePolygon()}} przyjmuje listę punktów i tworzy polilinię przechodzącą przez te punkty: |
|||
{{Code|code= |
|||
lshape_wire = Part.makePolygon([App.Vector(0, 5, 0), App.Vector(0, 0, 0), App.Vector(5, 0, 0)]) |
|||
}} |
|||
{{Top}} |
|||
<span id="Create_a_Bézier_curve"></span> |
|||
===Utwórz krzywą Béziera=== |
|||
Krzywe Béziera są używane do modelowania gładkich krzywych przy użyciu serii biegunów ''(punktów)'' i opcjonalnych wag. Poniższa funkcja tworzy krzywą {{incode|Part.BezierCurve()}} z serii punktów {{incode|FreeCAD.Vector()}}. Uwaga: przy "pobieraniu" i "ustawianiu" pojedynczego bieguna lub wagi, indeksy zaczynają się od 1, a nie od 0. |
|||
{{Code|code= |
|||
==== Creating a polygon ==== |
|||
A polygon is simply a wire with multiple straight edges. The makePolygon |
|||
function takes a list of points and creates a wire along those points: |
|||
<syntaxhighlight> |
|||
lshape_wire = Part.makePolygon([Base.Vector(0,5,0),Base.Vector(0,0,0),Base.Vector(5,0,0)]) |
|||
</syntaxhighlight> |
|||
==== Creating a Bezier curve ==== |
|||
Bézier curves are used to model smooth curves using a series of poles (points) and optional weights. The function below makes a Part.BezierCurve from a series of FreeCAD.Vector points. (Note: when "getting" and "setting" a single pole or weight indices start at 1, not 0.) |
|||
<syntaxhighlight> |
|||
def makeBCurveEdge(Points): |
def makeBCurveEdge(Points): |
||
geomCurve = Part.BezierCurve() |
geomCurve = Part.BezierCurve() |
||
| Line 275: | Line 345: | ||
edge = Part.Edge(geomCurve) |
edge = Part.Edge(geomCurve) |
||
return(edge) |
return(edge) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Creating a Plane ==== |
|||
<span id="Create_a_plane"></span> |
|||
A Plane is simply a flat rectangular surface. The method used to create one is |
|||
===Utwórz płaszczyznę=== |
|||
this: '''makePlane(length,width,[start_pnt,dir_normal])'''. By default |
|||
start_pnt = Vector(0,0,0) and dir_normal = Vector(0,0,1). Using dir_normal = Vector(0,0,1) |
|||
Płaszczyzna jest płaską prostokątną powierzchnią. Metoda używana do jej utworzenia to {{incode|makePlane(length, width, [start_pnt, dir_normal])}}. Domyślnie start_pnt = Vector(0, 0, 0) i dir_normal = Vector(0, 0, 1). Użycie dir_normal = Vector(0, 0, 1) spowoduje utworzenie płaszczyzny zwróconej w dodatnim kierunku osi Z, natomiast dir_normal = Vector(1, 0, 0) utworzy płaszczyznę zwróconą w dodatnim kierunku osi X: |
|||
will create the plane facing z axis, while dir_normal = Vector(1,0,0) will create the |
|||
plane facing x axis: |
|||
{{Code|code= |
|||
<syntaxhighlight> |
|||
plane = Part.makePlane(2,2) |
plane = Part.makePlane(2, 2) |
||
plane |
plane |
||
><Face object at 028AF990> |
> <Face object at 028AF990> |
||
plane = Part.makePlane(2,2, |
plane = Part.makePlane(2, 2, App.Vector(3, 0, 0), App.Vector(0, 1, 0)) |
||
plane.BoundBox |
plane.BoundBox |
||
> BoundBox (3, 0, 0, 5, 0, 2) |
> BoundBox (3, 0, 0, 5, 0, 2) |
||
}} |
|||
</syntaxhighlight> |
|||
BoundBox is a cuboid enclosing the plane with a diagonal starting at |
|||
(3,0,0) and ending at (5,0,2). Here the BoundBox thickness in y axis is zero, |
|||
since our shape is totally flat. |
|||
{{incode|BoundBox}} jest prostopadłościanem zamykającym płaszczyznę o przekątnej zaczynającej się w punkcie (3, 0, 0) i kończącej w punkcie (5, 0, 2). W tym przypadku grubość {{incode|BoundBox}} wzdłuż osi Y wynosi zero, ponieważ nasz kształt jest całkowicie płaski. |
|||
Note: makePlane only accepts Base.Vector() for start_pnt and dir_normal but not tuples |
|||
Uwaga: {{incode|makePlane()}} akceptuje tylko {{incode|App.Vector()}} dla start_pnt i dir_normal, a nie krotki. |
|||
==== Creating an ellipse ==== |
|||
{{Top}} |
|||
To create an ellipse there are several ways: |
|||
<span id="Create_an_ellipse"></span> |
|||
<syntaxhighlight> |
|||
===Utwórz elipsę=== |
|||
Istnieje kilka sposobów na utworzenie elipsy: |
|||
{{Code|code= |
|||
Part.Ellipse() |
Part.Ellipse() |
||
}} |
|||
</syntaxhighlight> |
|||
Creates an ellipse with major radius 2 and minor radius 1 with the center in (0,0,0) |
|||
Tworzy elipsę o wartości promienia głównego 2 i promienia mniejszego 1, o środku w punkcie (0, 0, 0). |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
Part.Ellipse(Ellipse) |
Part.Ellipse(Ellipse) |
||
}} |
|||
</syntaxhighlight> |
|||
Create a copy of the given ellipse |
|||
Tworzy kopię podanej elipsy. |
|||
<syntaxhighlight> |
|||
Part.Ellipse(S1,S2,Center) |
|||
{{Code|code= |
|||
</syntaxhighlight> |
|||
Part.Ellipse(S1, S2, Center) |
|||
Creates an ellipse centered on the point Center, where the plane of the |
|||
}} |
|||
ellipse is defined by Center, S1 and S2, its major axis is defined by |
|||
Center and S1, its major radius is the distance between Center and S1, |
|||
Tworzy elipsę wyśrodkowaną w punkcie Center, gdzie płaszczyzna elipsy jest określona przez Center, S1 i S2, jej oś główna jest określona przez Center i S1, jej promień główny jest odległością pomiędzy Center i S1, a jej promień mniejszy jest odległością pomiędzy S2 i osią główną. |
|||
and its minor radius is the distance between S2 and the major axis. |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
Part.Ellipse(Center,MajorRadius,MinorRadius) |
|||
Part.Ellipse(Center, MajorRadius, MinorRadius) |
|||
</syntaxhighlight> |
|||
}} |
|||
Creates an ellipse with major and minor radii MajorRadius and MinorRadius, |
|||
and located in the plane defined by Center and the normal (0,0,1) |
|||
Tworzy elipsę o promieniach MajorRadius i MinorRadius, znajdującą się w płaszczyźnie zdefiniowanej przez środek i normalną (0, 0, 1). |
|||
<syntaxhighlight> |
|||
eli = Part.Ellipse(Base.Vector(10,0,0),Base.Vector(0,5,0),Base.Vector(0,0,0)) |
|||
{{Code|code= |
|||
eli = Part.Ellipse(App.Vector(10, 0, 0), App.Vector(0, 5, 0), App.Vector(0, 0, 0)) |
|||
Part.show(eli.toShape()) |
Part.show(eli.toShape()) |
||
}} |
|||
</syntaxhighlight> |
|||
In the above code we have passed S1, S2 and center. Similarly to Arc, |
|||
Ellipse also creates an ellipse object but not edge, so we need to |
|||
convert it into edge using toShape() to display. |
|||
W powyższym kodzie przekazaliśmy S1, S2 i środek. Podobnie jak {{incode|Arc}}, {{incode|Ellipse}} tworzy obiekt elipsy, a nie krawędzi, więc musimy go przekonwertować na krawędź używając {{incode|toShape()}} do wyświetlenia. |
|||
Note: Arc only accepts Base.Vector() for points but not tuples |
|||
<syntaxhighlight> |
|||
Uwaga: {{incode|Ellipse()}} akceptuje tylko {{incode|App.Vector()}} dla punktów, a nie dla krotek. |
|||
eli = Part.Ellipse(Base.Vector(0,0,0),10,5) |
|||
{{Code|code= |
|||
eli = Part.Ellipse(App.Vector(0, 0, 0), 10, 5) |
|||
Part.show(eli.toShape()) |
Part.show(eli.toShape()) |
||
}} |
|||
</syntaxhighlight> |
|||
for the above Ellipse constructor we have passed center, MajorRadius and MinorRadius |
|||
Dla powyższego konstruktora elipsy przekazaliśmy center, MajorRadius oraz MinorRadius. |
|||
==== Creating a Torus ==== |
|||
{{Top}} |
|||
Using the method '''makeTorus(radius1,radius2,[pnt,dir,angle1,angle2,angle])'''. By |
|||
<span id="Create_a_torus"></span> |
|||
default pnt=Vector(0,0,0),dir=Vector(0,0,1),angle1=0,angle2=360 and angle=360. |
|||
===Utwórz torusa=== |
|||
Consider a torus as small circle sweeping along a big circle. Radius1 is the |
|||
radius of big cirlce, radius2 is the radius of small circle, pnt is the center |
|||
Używając {{incode|makeTorus(radius1, radius2, [pnt, dir, angle1, angle2, angle])}}. |
|||
of torus and dir is the normal direction. angle1 and angle2 are angles in |
|||
Domyślnie pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1), angle1 = 0, angle2 = 360 i angle = 360. |
|||
radians for the small circle, the last parameter angle is to make a section of |
|||
Rozważmy torus jako małe koło, które porusza się po dużym okręgu. Radius1 jest promieniem dużego okręgu, radius2 jest promieniem małego okręgu, pnt jest środkiem torusa, a dir jest kierunkiem normalnej. angle1 i angle2 są kątami w stopniach dla małego okręgu; ostatni parametr angle jest po to, by zrobić przekrój torusa: |
|||
the torus: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
torus = Part.makeTorus(10, 2) |
torus = Part.makeTorus(10, 2) |
||
}} |
|||
</syntaxhighlight> |
|||
The above code will create a torus with diameter 20(radius 10) and thickness 4 |
|||
(small cirlce radius 2) |
|||
<syntaxhighlight> |
|||
tor=Part.makeTorus(10,5,Base.Vector(0,0,0),Base.Vector(0,0,1),0,180) |
|||
</syntaxhighlight> |
|||
The above code will create a slice of the torus |
|||
<syntaxhighlight> |
|||
tor=Part.makeTorus(10,5,Base.Vector(0,0,0),Base.Vector(0,0,1),0,360,180) |
|||
</syntaxhighlight> |
|||
The above code will create a semi torus, only the last parameter is changed |
|||
i.e the angle and remaining angles are defaults. Giving the angle 180 will |
|||
create the torus from 0 to 180, that is, a half torus. |
|||
Powyższy kod utworzy torus o średnicy {{Value|20}} ''(promień 10)'' i grubości {{Value|4}} ''(promień małego okręgu 2)'' |
|||
==== Creating a box or cuboid ==== |
|||
Using '''makeBox(length,width,height,[pnt,dir])'''. |
|||
{{Code|code= |
|||
By default pnt=Vector(0,0,0) and dir=Vector(0,0,1) |
|||
tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180) |
|||
<syntaxhighlight> |
|||
}} |
|||
box = Part.makeBox(10,10,10) |
|||
Powyższy kod utworzy wycinek torusa. |
|||
{{Code|code= |
|||
tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 360, 180) |
|||
}} |
|||
Powyższy kod utworzy połowę torusa; tylko ostatni parametr jest zmieniony, tzn. pozostałe kąty są domyślne. Nadanie kąta 180 spowoduje utworzenie torusa od 0 do 180, czyli jego połowę. |
|||
{{Top}} |
|||
<span id="Create_a_box_or_cuboid"></span> |
|||
===Utwórz sześcian lub prostopadłościan=== |
|||
Przy użyciu {{incode|makeBox(length, width, height, [pnt, dir])}}. |
|||
Domyślnie pnt = Vector(0, 0, 0) i dir = Vector(0, 0, 1). |
|||
{{Code|code= |
|||
box = Part.makeBox(10, 10, 10) |
|||
len(box.Vertexes) |
len(box.Vertexes) |
||
> 8 |
> 8 |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Creating a Sphere ==== |
|||
<span id="Create_a_sphere"></span> |
|||
Using '''makeSphere(radius,[pnt, dir, angle1,angle2,angle3])'''. By default |
|||
===Utwórz sferę=== |
|||
pnt=Vector(0,0,0), dir=Vector(0,0,1), angle1=-90, angle2=90 and angle3=360. |
|||
angle1 and angle2 are the vertical minimum and maximum of the sphere, angle3 |
|||
Przy użyciu {{incode|makeSphere(radius, [pnt, dir, angle1, angle2, angle3])}}. Domyślnie pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1), angle1 = -90, angle2 = 90 i angle3 = 360. |
|||
is the sphere diameter itself. |
|||
Kąt1 i kąt2 to pionowe minimum i maksimum sfery, kąt3 to średnica sfery. |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
sphere = Part.makeSphere(10) |
sphere = Part.makeSphere(10) |
||
hemisphere = Part.makeSphere(10, |
hemisphere = Part.makeSphere(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), -90, 90, 180) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Creating a Cylinder ==== |
|||
<span id="Create_a_cylinder"></span> |
|||
Using '''makeCylinder(radius,height,[pnt,dir,angle])'''. By default |
|||
===Utwórz walec=== |
|||
pnt=Vector(0,0,0),dir=Vector(0,0,1) and angle=360 |
|||
<syntaxhighlight> |
|||
cylinder = Part.makeCylinder(5,20) |
|||
partCylinder = Part.makeCylinder(5,20,Base.Vector(20,0,0),Base.Vector(0,0,1),180) |
|||
</syntaxhighlight> |
|||
==== Creating a Cone ==== |
|||
Using '''makeCone(radius1,radius2,height,[pnt,dir,angle])'''. By default |
|||
pnt=Vector(0,0,0), dir=Vector(0,0,1) and angle=360 |
|||
<syntaxhighlight> |
|||
cone = Part.makeCone(10,0,20) |
|||
semicone = Part.makeCone(10,0,20,Base.Vector(20,0,0),Base.Vector(0,0,1),180) |
|||
</syntaxhighlight> |
|||
== Modifying shapes == |
|||
There are several ways to modify shapes. Some are simple transformation operations |
|||
such as moving or rotating shapes, other are more complex, such as unioning and |
|||
subtracting one shape from another. Be aware that |
|||
Przy użyciu {{incode|makeCylinder(radius, height, [pnt, dir, angle])}}. Domyślnie pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1) i angle = 360. |
|||
=== Transform operations === |
|||
{{Code|code= |
|||
==== Translating a shape ==== |
|||
cylinder = Part.makeCylinder(5, 20) |
|||
Translating is the act of moving a shape from one place to another. |
|||
partCylinder = Part.makeCylinder(5, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180) |
|||
Any shape (edge, face, cube, etc...) can be translated the same way: |
|||
}} |
|||
<syntaxhighlight> |
|||
{{Top}} |
|||
myShape = Part.makeBox(2,2,2) |
|||
<span id="Create_a_cone"></span> |
|||
myShape.translate(Base.Vector(2,0,0)) |
|||
===Utwórz stożek=== |
|||
</syntaxhighlight> |
|||
This will move our shape "myShape" 2 units in the x direction. |
|||
Przy użyciu {{incode|makeCone(radius1, radius2, height, [pnt, dir, angle])}}. Domyślnie pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1) i angle = 360. |
|||
==== Rotating a shape ==== |
|||
To rotate a shape, you need to specify the rotation center, the axis, |
|||
and the rotation angle: |
|||
<syntaxhighlight> |
|||
myShape.rotate(Vector(0,0,0),Vector(0,0,1),180) |
|||
</syntaxhighlight> |
|||
The above code will rotate the shape 180 degrees around the Z Axis. |
|||
{{Code|code= |
|||
==== Generic transformations with matrixes ==== |
|||
cone = Part.makeCone(10, 0, 20) |
|||
A matrix is a very convenient way to store transformations in the 3D |
|||
semicone = Part.makeCone(10, 0, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180) |
|||
world. In a single matrix, you can set translation, rotation and scaling |
|||
}} |
|||
values to be applied to an object. For example: |
|||
{{Top}} |
|||
<syntaxhighlight> |
|||
<span id="Modify_shapes"></span> |
|||
myMat = Base.Matrix() |
|||
==Modyfikuj kształty== |
|||
myMat.move(Base.Vector(2,0,0)) |
|||
Kształty można modyfikować na kilka sposobów. Niektóre z nich to proste operacje przekształcania, takie jak przesuwanie lub obracanie kształtów, inne są bardziej złożone, np. łączenie i odejmowanie jednego kształtu od drugiego. |
|||
{{Top}} |
|||
<span id="Transform_operations"></span> |
|||
==Operacje przekształcenia== |
|||
<span id="Translate_a_shape"></span> |
|||
===Przekształcanie kształtu=== |
|||
Przesunięcie to czynność polegająca na przeniesieniu kształtu z jednego miejsca w drugie. Każdy kształt ''(krawędź, ściana, sześcian, itd...)'' może być przesunięty w ten sam sposób: |
|||
{{Code|code= |
|||
myShape = Part.makeBox(2, 2, 2) |
|||
myShape.translate(App.Vector(2, 0, 0)) |
|||
}} |
|||
Spowoduje to przesunięcie naszego kształtu "myShape" o 2 jednostki w kierunku X. |
|||
{{Top}} |
|||
<span id="Rotate_a_shape"></span> |
|||
===Obrót kształtu=== |
|||
Aby obrócić kształt, należy określić środek obrotu, oś i kąt obrotu: |
|||
{{Code|code= |
|||
myShape.rotate(App.Vector(0, 0, 0),App.Vector(0, 0, 1), 180) |
|||
}} |
|||
Powyższy kod obróci kształt o 180 stopni wokół osi Z. |
|||
{{Top}} |
|||
<span id="Matrix_transformations"></span> |
|||
===Przekształcenia macierzowe=== |
|||
Macierz jest bardzo wygodnym sposobem przechowywania przekształceń w świecie 3D. W pojedynczej macierzy można ustawić wartości przesunięcia, obrotu i skalowania, które mają być zastosowane do obiektu. Na przykład: |
|||
{{Code|code= |
|||
myMat = App.Matrix() |
|||
myMat.move(App.Vector(2, 0, 0)) |
|||
myMat.rotateZ(math.pi/2) |
myMat.rotateZ(math.pi/2) |
||
}} |
|||
</syntaxhighlight> |
|||
Note: FreeCAD matrixes work in radians. Also, almost all matrix operations |
|||
Uwaga: Macierze FreeCAD działają w radianach. Ponadto, prawie wszystkie operacje na macierzach, które przyjmują wektor, mogą również przyjmować trzy liczby, więc te dwie linie robią to samo: |
|||
that take a vector can also take 3 numbers, so those 2 lines do the same thing: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
myMat.move(2,0,0) |
|||
myMat.move |
myMat.move(2, 0, 0) |
||
myMat.move(App.Vector(2, 0, 0)) |
|||
</syntaxhighlight> |
|||
}} |
|||
When our matrix is set, we can apply it to our shape. FreeCAD provides 2 |
|||
methods to do that: transformShape() and transformGeometry(). The difference |
|||
Kiedy nasza macierz jest już ustalona, możemy ją zastosować do naszego kształtu. FreeCAD udostępnia dwie metody, aby to zrobić: {{incode|transformShape()}} oraz {{incode|transformGeometry()}}. Różnica jest taka, że w przypadku pierwszej z nich mamy pewność, że nie wystąpią żadne deformacje ''(patrz poniżej [[#Skalowanie_kszta.C5.82tu|Skalowanie kształtu]])''. Naszą transformację możemy zastosować w ten sposób: |
|||
is that with the first one, you are sure that no deformations will occur (see |
|||
"scaling a shape" below). So we can apply our transformation like this: |
|||
{{Code|code= |
|||
<syntaxhighlight> |
|||
myShape.transformShape(myMat) |
|||
}} |
|||
</syntaxhighlight> |
|||
or |
|||
lub |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
myShape.transformGeometry(myMat) |
myShape.transformGeometry(myMat) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Scaling a shape ==== |
|||
<span id="Scale_a_shape"></span> |
|||
Scaling a shape is a more dangerous operation because, unlike translation |
|||
===Skalowanie kształtu=== |
|||
or rotation, scaling non-uniformly (with different values for x, y and z) |
|||
can modify the structure of the shape. For example, scaling a circle with |
|||
Skalowanie kształtu jest bardziej niebezpieczną operacją, ponieważ w przeciwieństwie do przesunięcia czy obrotu, skalowanie nierównomierne ''(z różnymi wartościami dla X, Y i Z)'' może zmienić strukturę kształtu. Na przykład, skalowanie koła z większą wartością w poziomie niż w pionie przekształci je w elipsę, która zachowuje się matematycznie zupełnie inaczej. Do skalowania nie możemy użyć metody {{incode|transformShape()}}, musimy użyć {{incode|transformGeometry()}}: |
|||
a higher value horizontally than vertically will transform it into an |
|||
ellipse, which behaves mathematically very differenty. For scaling, we |
|||
{{Code|code= |
|||
can't use the transformShape, we must use transformGeometry(): |
|||
myMat = App.Matrix() |
|||
<syntaxhighlight> |
|||
myMat |
myMat.scale(2, 1, 1) |
||
myMat.scale(2,1,1) |
|||
myShape=myShape.transformGeometry(myMat) |
myShape=myShape.transformGeometry(myMat) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
=== Boolean Operations === |
|||
<span id="Boolean_operations"></span> |
|||
==Operacje logiczne== |
|||
= |
<span id="Subtraction"></span> |
||
===Operacja odjęcia=== |
|||
Subtracting a shape from another one is called "cut" in OCC/FreeCAD jargon |
|||
and is done like this: |
|||
Odejmowanie kształtu od innego nazywane jest w FreeCAD "cięciem" i odbywa się w następujący sposób: |
|||
<syntaxhighlight> |
|||
cylinder = Part.makeCylinder(3,10,Base.Vector(0,0,0),Base.Vector(1,0,0)) |
|||
{{Code|code= |
|||
sphere = Part.makeSphere(5,Base.Vector(5,0,0)) |
|||
cylinder = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0)) |
|||
sphere = Part.makeSphere(5, App.Vector(5, 0, 0)) |
|||
diff = cylinder.cut(sphere) |
diff = cylinder.cut(sphere) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Intersection ==== |
|||
<span id="Intersection"></span> |
|||
The same way, the intersection between 2 shapes is called "common" and is done |
|||
===Przecięcie=== |
|||
this way: |
|||
<syntaxhighlight> |
|||
W ten sam sposób przecięcie dwóch kształtów nazywane jest "częścią wspólną" i jest wykonywane w ten sposób: |
|||
cylinder1 = Part.makeCylinder(3,10,Base.Vector(0,0,0),Base.Vector(1,0,0)) |
|||
cylinder2 = Part.makeCylinder(3,10,Base.Vector(5,0,-5),Base.Vector(0,0,1)) |
|||
{{Code|code= |
|||
cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0)) |
|||
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1)) |
|||
common = cylinder1.common(cylinder2) |
common = cylinder1.common(cylinder2) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Union ==== |
|||
<span id="Union"></span> |
|||
Union is called "fuse" and works the same way: |
|||
===Połączenie=== |
|||
<syntaxhighlight> |
|||
cylinder1 = Part.makeCylinder(3,10,Base.Vector(0,0,0),Base.Vector(1,0,0)) |
|||
Połączenie nazywa się "scaleniem" i działa w ten sam sposób: |
|||
cylinder2 = Part.makeCylinder(3,10,Base.Vector(5,0,-5),Base.Vector(0,0,1)) |
|||
{{Code|code= |
|||
cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0)) |
|||
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1)) |
|||
fuse = cylinder1.fuse(cylinder2) |
fuse = cylinder1.fuse(cylinder2) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Section ==== |
|||
<span id="Section"></span> |
|||
A Section is the intersection between a solid shape and a plane shape. |
|||
===Przekrój=== |
|||
It will return an intersection curve, a compound with edges |
|||
<syntaxhighlight> |
|||
"Przekrój" jest punktem przecięcia bryły z płaszczyzną. Zwraca krzywą przecięcia, krzywą złożoną utworzoną z krawędzi. |
|||
cylinder1 = Part.makeCylinder(3,10,Base.Vector(0,0,0),Base.Vector(1,0,0)) |
|||
cylinder2 = Part.makeCylinder(3,10,Base.Vector(5,0,-5),Base.Vector(0,0,1)) |
|||
{{Code|code= |
|||
cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0)) |
|||
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1)) |
|||
section = cylinder1.section(cylinder2) |
section = cylinder1.section(cylinder2) |
||
section.Wires |
section.Wires |
||
| Line 488: | Line 601: | ||
<Edge object at 0D86DE18>, <Edge object at 0D9B8E80>, <Edge object at 012A3640>, |
<Edge object at 0D86DE18>, <Edge object at 0D9B8E80>, <Edge object at 012A3640>, |
||
<Edge object at 0D8F4BB0>] |
<Edge object at 0D8F4BB0>] |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
==== Extrusion ==== |
|||
<span id="Extrusion"></span> |
|||
Extrusion is the act of "pushing" a flat shape in a certain direction resulting in |
|||
===Wyciąganie=== |
|||
a solid body. Think of a circle becoming a tube by "pushing it out": |
|||
<syntaxhighlight> |
|||
Wyciąganie to czynność "wypychania" płaskiego kształtu w określonym kierunku, w wyniku czego powstaje pełna bryła. Pomyśl o kole, które staje się rurką poprzez "wypychanie" go na zewnątrz: |
|||
{{Code|code= |
|||
circle = Part.makeCircle(10) |
circle = Part.makeCircle(10) |
||
tube = circle.extrude( |
tube = circle.extrude(App.Vector(0, 0, 2)) |
||
}} |
|||
</syntaxhighlight> |
|||
If your circle is hollow, you will obtain a hollow tube. If your circle is actually |
|||
Jeśli twój okrąg jest pusty, otrzymasz pustą rurkę. Jeśli twój okrąg jest w rzeczywistości dyskiem z wypełnioną powierzchnią, otrzymasz pełny walec: |
|||
a disc, with a filled face, you will obtain a solid cylinder: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
wire = Part.Wire(circle) |
wire = Part.Wire(circle) |
||
disc = Part. |
disc = Part.Face(wire) |
||
cylinder = disc.extrude( |
cylinder = disc.extrude(App.Vector(0, 0, 2)) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
== Exploring shapes == |
|||
<span id="Explore_shapes"></span> |
|||
You can easily explore the topological data structure: |
|||
==Badanie kształtów== |
|||
<syntaxhighlight> |
|||
Możesz łatwo zbadać topologiczną strukturę danych: |
|||
{{Code|code= |
|||
import Part |
import Part |
||
b = Part.makeBox(100,100,100) |
b = Part.makeBox(100, 100, 100) |
||
b.Wires |
b.Wires |
||
w = b.Wires[0] |
w = b.Wires[0] |
||
| Line 519: | Line 640: | ||
v = e.Vertexes[0] |
v = e.Vertexes[0] |
||
v.Point |
v.Point |
||
}} |
|||
</syntaxhighlight> |
|||
By typing the lines above in the python interpreter, you will gain a good |
|||
understanding of the structure of Part objects. Here, our makeBox() command |
|||
created a solid shape. This solid, like all Part solids, contains faces. |
|||
Faces always contain wires, which are lists of edges that border the face. |
|||
Each face has at least one closed wire (it can have more if the face has a hole). |
|||
In the wire, we can look at each edge separately, and inside each edge, we can |
|||
see the vertexes. Straight edges have only two vertexes, obviously. |
|||
Wpisując powyższe linie w interpreterze Python, uzyskasz dobre zrozumienie struktury obiektów Część. Tutaj, nasze polecenie {{incode|makeBox()}} utworzyło bryłę. Ta bryła, jak wszystkie bryły typu Część, zawiera ściany. Ściany zawsze zawierają linie łamane ''(polilinie)'', które są listą krawędzi ograniczających daną ścianę. Każda ściana ma co najmniej jedną zamkniętą linię łamaną ''(może mieć ich więcej, jeśli posiada otwór)''. W liniach łamanych możemy oglądać każdą krawędź z osobna, a wewnątrz każdej krawędzi możemy zobaczyć wierzchołki. Proste krawędzie mają oczywiście tylko dwa wierzchołki. |
|||
=== Edge analysis === |
|||
{{Top}} |
|||
In case of an edge, which is an arbitrary curve, it's most likely you want to |
|||
<span id="Edge_analysis"></span> |
|||
do a discretization. In FreeCAD the edges are parametrized by their lengths. |
|||
===Analiza krawędzi=== |
|||
That means you can walk an edge/curve by its length: |
|||
<syntaxhighlight> |
|||
W przypadku krawędzi, która jest arbitralną krzywą, najprawdopodobniej chcesz dokonać dyskretyzacji. W FreeCAD krawędzie są parametryzowane przez ich długości. Oznacza to, że możesz przejść po krawędzi/krzywej przez jej długość: |
|||
{{Code|code= |
|||
import Part |
import Part |
||
box = Part.makeBox(100,100,100) |
box = Part.makeBox(100, 100, 100) |
||
anEdge = box.Edges[0] |
anEdge = box.Edges[0] |
||
print |
print(anEdge.Length) |
||
}} |
|||
</syntaxhighlight> |
|||
Now you can access a lot of properties of the edge by using the length as a |
|||
Teraz możesz uzyskać dostęp do wielu właściwości krawędzi, używając długości jako pozycji. Oznacza to, że jeśli krawędź ma długość 100mm, to pozycja początkowa wynosi 0, a końcowa 100. |
|||
position. That means if the edge is 100mm long the start position is 0 and |
|||
the end position 100. |
|||
{{Code|code= |
|||
<syntaxhighlight> |
|||
anEdge.tangentAt(0.0) # tangent direction at the beginning |
anEdge.tangentAt(0.0) # tangent direction at the beginning |
||
anEdge.valueAt(0.0) # Point at the beginning |
anEdge.valueAt(0.0) # Point at the beginning |
||
anEdge.valueAt(100.0) # Point at the end of the edge |
anEdge.valueAt(100.0) # Point at the end of the edge |
||
anEdge.derivative1At(50.0) # first derivative of the curve in the middle |
anEdge.derivative1At(50.0) # first derivative of the curve in the middle |
||
anEdge.derivative2At(50.0) # second derivative of the curve in the middle |
anEdge.derivative2At(50.0) # second derivative of the curve in the middle |
||
anEdge.derivative3At(50.0) # third derivative of the curve in the middle |
anEdge.derivative3At(50.0) # third derivative of the curve in the middle |
||
anEdge.centerOfCurvatureAt(50) # center of the curvature for that position |
anEdge.centerOfCurvatureAt(50) # center of the curvature for that position |
||
anEdge.curvatureAt(50.0) # the curvature |
anEdge.curvatureAt(50.0) # the curvature |
||
anEdge.normalAt(50) # normal vector at that position (if defined) |
anEdge.normalAt(50) # normal vector at that position (if defined) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
=== Using the selection === |
|||
<span id="Use_a_selection"></span> |
|||
Here we see now how we can use the selection the user did in the viewer. |
|||
===Użycie zaznaczenia=== |
|||
First of all we create a box and shows it in the viewer |
|||
<syntaxhighlight> |
|||
Tutaj widzimy teraz, jak możemy wykorzystać wybór, który użytkownik przeprowadził w przeglądarce. |
|||
Najpierw tworzymy sześcian i pokazujemy go w przeglądarce. |
|||
{{Code|code= |
|||
import Part |
import Part |
||
Part.show(Part.makeBox(100,100,100)) |
Part.show(Part.makeBox(100, 100, 100)) |
||
Gui.SendMsgToActiveView("ViewFit") |
Gui.SendMsgToActiveView("ViewFit") |
||
}} |
|||
</syntaxhighlight> |
|||
Select now some faces or edges. With this script you can |
|||
Teraz wybierz kilka ścian lub krawędzi. Za pomocą tego skryptu możesz przejść po wszystkich zaznaczonych obiektach i ich elementach podrzędnych: |
|||
iterate all selected objects and their sub elements: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
for o in Gui.Selection.getSelectionEx(): |
for o in Gui.Selection.getSelectionEx(): |
||
print(o.ObjectName) |
|||
for s in o.SubElementNames: |
|||
print("name: ", s) |
|||
for s in o.SubObjects: |
|||
print("object: ", s) |
|||
}} |
|||
</syntaxhighlight> |
|||
Select some edges and this script will calculate the length: |
|||
Wybierz kilka krawędzi, a ten skrypt obliczy ich długość: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
length = 0.0 |
length = 0.0 |
||
for o in Gui.Selection.getSelectionEx(): |
for o in Gui.Selection.getSelectionEx(): |
||
for s in o.SubObjects: |
|||
length += s.Length |
|||
print "Length of the selected edges:" ,length |
|||
print("Length of the selected edges: ", length) |
|||
</syntaxhighlight> |
|||
}} |
|||
== Complete example: The OCC bottle == |
|||
{{Top}} |
|||
A typical example found on the |
|||
<span id="Example:_The_OCC_bottle"></span> |
|||
[http://www.opencascade.org/org/gettingstarted/appli/ OpenCasCade Getting Started Page] |
|||
==Przykład: Butelka OCC== |
|||
is how to build a bottle. This is a good exercise for FreeCAD too. In fact, |
|||
you can follow our example below and the OCC page simultaneously, you will |
|||
Typowym przykładem, który można znaleźć na stronie [https://www.opencascade.com/doc/occt-6.9.0/overview/html/occt__tutorial.html OpenCasCade Technology] jest sposób na zbudowanie butelki. Jest to dobre ćwiczenie również dla programu FreeCAD. W rzeczywistości, jeśli będziesz śledził nasz przykład poniżej i stronę OCC jednocześnie, zobaczysz jak dobrze struktury OCC są zaimplementowane w FreeCAD. Skrypt jest dołączony do instalacji FreeCAD ''(w folderze {{FileName|Mod/Part}})'' i może być wywołany z interpretera Python przez wpisanie: |
|||
understand well how OCC structures are implemented in FreeCAD. The complete script |
|||
below is also included in FreeCAD installation (inside the Mod/Part folder) and |
|||
{{Code|code= |
|||
can be called from the python interpreter by typing: |
|||
<syntaxhighlight> |
|||
import Part |
import Part |
||
import MakeBottle |
import MakeBottle |
||
bottle = MakeBottle.makeBottle() |
bottle = MakeBottle.makeBottle() |
||
Part.show(bottle) |
Part.show(bottle) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
=== The complete script === |
|||
<span id="The_script"></span> |
|||
Here is the complete MakeBottle script: |
|||
===Skrypt=== |
|||
<syntaxhighlight> |
|||
import Part, FreeCAD, math |
|||
from FreeCAD import Base |
|||
def makeBottle(myWidth=50.0, myHeight=70.0, myThickness=30.0): |
|||
aPnt1=Base.Vector(-myWidth/2.,0,0) |
|||
aPnt2=Base.Vector(-myWidth/2.,-myThickness/4.,0) |
|||
aPnt3=Base.Vector(0,-myThickness/2.,0) |
|||
aPnt4=Base.Vector(myWidth/2.,-myThickness/4.,0) |
|||
aPnt5=Base.Vector(myWidth/2.,0,0) |
|||
aArcOfCircle = Part.Arc(aPnt2,aPnt3,aPnt4) |
|||
aSegment1=Part.Line(aPnt1,aPnt2) |
|||
aSegment2=Part.Line(aPnt4,aPnt5) |
|||
aEdge1=aSegment1.toShape() |
|||
aEdge2=aArcOfCircle.toShape() |
|||
aEdge3=aSegment2.toShape() |
|||
aWire=Part.Wire([aEdge1,aEdge2,aEdge3]) |
|||
aTrsf=Base.Matrix() |
|||
aTrsf.rotateZ(math.pi) # rotate around the z-axis |
|||
aMirroredWire=aWire.transformGeometry(aTrsf) |
|||
myWireProfile=Part.Wire([aWire,aMirroredWire]) |
|||
myFaceProfile=Part.Face(myWireProfile) |
|||
aPrismVec=Base.Vector(0,0,myHeight) |
|||
myBody=myFaceProfile.extrude(aPrismVec) |
|||
myBody=myBody.makeFillet(myThickness/12.0,myBody.Edges) |
|||
neckLocation=Base.Vector(0,0,myHeight) |
|||
neckNormal=Base.Vector(0,0,1) |
|||
myNeckRadius = myThickness / 4. |
|||
myNeckHeight = myHeight / 10 |
|||
myNeck = Part.makeCylinder(myNeckRadius,myNeckHeight,neckLocation,neckNormal) |
|||
myBody = myBody.fuse(myNeck) |
|||
faceToRemove = 0 |
|||
zMax = -1.0 |
|||
for xp in myBody.Faces: |
|||
try: |
|||
surf = xp.Surface |
|||
if type(surf) == Part.Plane: |
|||
z = surf.Position.z |
|||
if z > zMax: |
|||
zMax = z |
|||
faceToRemove = xp |
|||
except: |
|||
continue |
|||
myBody = myBody.makeThickness([faceToRemove],-myThickness/50 , 1.e-3) |
|||
return myBody |
|||
</syntaxhighlight> |
|||
=== Detailed explanation === |
|||
<syntaxhighlight> |
|||
import Part, FreeCAD, math |
|||
from FreeCAD import Base |
|||
</syntaxhighlight> |
|||
We will need,of course, the Part module, but also the FreeCAD.Base module, |
|||
which contains basic FreeCAD structures like vectors and matrixes. |
|||
<syntaxhighlight> |
|||
def makeBottle(myWidth=50.0, myHeight=70.0, myThickness=30.0): |
|||
aPnt1=Base.Vector(-myWidth/2.,0,0) |
|||
aPnt2=Base.Vector(-myWidth/2.,-myThickness/4.,0) |
|||
aPnt3=Base.Vector(0,-myThickness/2.,0) |
|||
aPnt4=Base.Vector(myWidth/2.,-myThickness/4.,0) |
|||
aPnt5=Base.Vector(myWidth/2.,0,0) |
|||
</syntaxhighlight> |
|||
Here we define our makeBottle function. This function can be called without |
|||
arguments, like we did above, in which case default values for width, height, |
|||
and thickness will be used. Then, we define a couple of points that will be used |
|||
for building our base profile. |
|||
<syntaxhighlight> |
|||
aArcOfCircle = Part.Arc(aPnt2,aPnt3,aPnt4) |
|||
aSegment1=Part.Line(aPnt1,aPnt2) |
|||
aSegment2=Part.Line(aPnt4,aPnt5) |
|||
</syntaxhighlight> |
|||
Here we actually define the geometry: an arc, made of 3 points, and two |
|||
line segments, made of 2 points. |
|||
<syntaxhighlight> |
|||
aEdge1=aSegment1.toShape() |
|||
aEdge2=aArcOfCircle.toShape() |
|||
aEdge3=aSegment2.toShape() |
|||
aWire=Part.Wire([aEdge1,aEdge2,aEdge3]) |
|||
</syntaxhighlight> |
|||
Remember the difference between geometry and shapes? Here we build |
|||
shapes out of our construction geometry. 3 edges (edges can be straight |
|||
or curved), then a wire made of those three edges. |
|||
<syntaxhighlight> |
|||
aTrsf=Base.Matrix() |
|||
aTrsf.rotateZ(math.pi) # rotate around the z-axis |
|||
aMirroredWire=aWire.transformGeometry(aTrsf) |
|||
myWireProfile=Part.Wire([aWire,aMirroredWire]) |
|||
</syntaxhighlight> |
|||
Until now we built only a half profile. Easier than building the whole profile |
|||
the same way, we can just mirror what we did, and glue both halfs together. |
|||
So we first create a matrix. A matrix is a very common way to apply transformations |
|||
to objects in the 3D world, since it can contain in one structure all basic |
|||
transformations that 3D objects can suffer (move, rotate and scale). Here, |
|||
after we create the matrix, we mirror it, and we create a copy of our wire |
|||
with that transformation matrix applied to it. We now have two wires, and |
|||
we can make a third wire out of them, since wires are actually lists of edges. |
|||
<syntaxhighlight> |
|||
myFaceProfile=Part.Face(myWireProfile) |
|||
aPrismVec=Base.Vector(0,0,myHeight) |
|||
myBody=myFaceProfile.extrude(aPrismVec) |
|||
myBody=myBody.makeFillet(myThickness/12.0,myBody.Edges) |
|||
</syntaxhighlight> |
|||
Now that we have a closed wire, it can be turned into a face. Once we have a face, |
|||
we can extrude it. Doing so, we actually made a solid. Then we apply a nice little |
|||
fillet to our object because we care about good design, don't we? |
|||
<syntaxhighlight> |
|||
neckLocation=Base.Vector(0,0,myHeight) |
|||
neckNormal=Base.Vector(0,0,1) |
|||
myNeckRadius = myThickness / 4. |
|||
myNeckHeight = myHeight / 10 |
|||
myNeck = Part.makeCylinder(myNeckRadius,myNeckHeight,neckLocation,neckNormal) |
|||
</syntaxhighlight> |
|||
Then, the body of our bottle is made, we still need to create a neck. So we |
|||
make a new solid, with a cylinder. |
|||
<syntaxhighlight> |
|||
myBody = myBody.fuse(myNeck) |
|||
</syntaxhighlight> |
|||
The fuse operation, which in other apps is sometimes called union, is very |
|||
powerful. It will take care of gluing what needs to be glued and remove parts that |
|||
need to be removed. |
|||
<syntaxhighlight> |
|||
return myBody |
|||
</syntaxhighlight> |
|||
Then, we return our Part solid as the result of our function. That Part solid, |
|||
like any other Part shape, can be attributed to an object in a FreeCAD document, with: |
|||
<syntaxhighlight> |
|||
myObject = FreeCAD.ActiveDocument.addObject("Part::Feature","myObject") |
|||
myObject.Shape = bottle |
|||
</syntaxhighlight> |
|||
or, more simple: |
|||
<syntaxhighlight> |
|||
Part.show(bottle) |
|||
</syntaxhighlight> |
|||
==Box pierced== |
|||
Here a complete example of building a box pierced. |
|||
Na potrzeby tego poradnika rozważymy okrojoną wersję skryptu. W tej wersji butelka nie będzie wydrążona, a szyjka butelki nie będzie gwintowana. |
|||
The construction is done side by side and when the cube is finished, it is hollowed out of a cylinder through. |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
import Draft, Part, FreeCAD, math, PartGui, FreeCADGui, PyQt4 |
|||
import FreeCAD as App |
|||
import Part, math |
|||
from FreeCAD import Base |
|||
def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0): |
|||
aPnt1=App.Vector(-myWidth / 2., 0, 0) |
|||
aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0) |
|||
aPnt3=App.Vector(0, -myThickness / 2., 0) |
|||
aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0) |
|||
aPnt5=App.Vector(myWidth / 2., 0, 0) |
|||
aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4) |
|||
aSegment1=Part.LineSegment(aPnt1, aPnt2) |
|||
aSegment2=Part.LineSegment(aPnt4, aPnt5) |
|||
aEdge1=aSegment1.toShape() |
|||
aEdge2=aArcOfCircle.toShape() |
|||
aEdge3=aSegment2.toShape() |
|||
aWire=Part.Wire([aEdge1, aEdge2, aEdge3]) |
|||
aTrsf=App.Matrix() |
|||
aTrsf.rotateZ(math.pi) # rotate around the z-axis |
|||
aMirroredWire=aWire.copy() |
|||
aMirroredWire.transformShape(aTrsf) |
|||
myWireProfile=Part.Wire([aWire, aMirroredWire]) |
|||
myFaceProfile=Part.Face(myWireProfile) |
|||
aPrismVec=App.Vector(0, 0, myHeight) |
|||
myBody=myFaceProfile.extrude(aPrismVec) |
|||
myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges) |
|||
neckLocation=App.Vector(0, 0, myHeight) |
|||
neckNormal=App.Vector(0, 0, 1) |
|||
myNeckRadius = myThickness / 4. |
|||
myNeckHeight = myHeight / 10. |
|||
myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal) |
|||
myBody = myBody.fuse(myNeck) |
|||
return myBody |
|||
el = makeBottleTut() |
|||
Part.show(el) |
|||
}} |
|||
{{Top}} |
|||
<span id="Detailed_explanation"></span> |
|||
===Szczegółowe objaśnienia=== |
|||
{{Code|code= |
|||
import FreeCAD as App |
|||
import Part, math |
|||
}} |
|||
Potrzebny nam będzie oczywiście moduł {{incode|FreeCAD}}, ale także moduł {{incode|Part}}. |
|||
{{Code|code= |
|||
def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0): |
|||
aPnt1=App.Vector(-myWidth / 2., 0, 0) |
|||
aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0) |
|||
aPnt3=App.Vector(0, -myThickness / 2., 0) |
|||
aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0) |
|||
aPnt5=App.Vector(myWidth / 2., 0, 0) |
|||
}} |
|||
Tutaj definiujemy naszą funkcję {{incode|makeBottleTut}}. Funkcja ta może być wywołana bez argumentów, tak jak zrobiliśmy to powyżej, w tym przypadku zostaną użyte domyślne wartości dla szerokości, wysokości i grubości. Następnie definiujemy kilka punktów, które zostaną użyte do budowy naszego profilu bazowego. |
|||
{{Code|code= |
|||
... |
|||
aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4) |
|||
aSegment1=Part.LineSegment(aPnt1, aPnt2) |
|||
aSegment2=Part.LineSegment(aPnt4, aPnt5) |
|||
}} |
|||
Tutaj definiujemy geometrię: łuk, złożony z trzech punktów, oraz dwa odcinki linii, złożone z dwóch punktów. |
|||
{{Code|code= |
|||
... |
|||
aEdge1=aSegment1.toShape() |
|||
aEdge2=aArcOfCircle.toShape() |
|||
aEdge3=aSegment2.toShape() |
|||
aWire=Part.Wire([aEdge1, aEdge2, aEdge3]) |
|||
}} |
|||
Pamiętasz różnicę między geometrią a kształtami? Tutaj budujemy kształty z naszej geometrii konstrukcyjnej. Trzy krawędzie ''(krawędzie mogą być proste lub zakrzywione)'', następnie linia łamana wykonana z tych trzech krawędzi. |
|||
{{Code|code= |
|||
... |
|||
aTrsf=App.Matrix() |
|||
aTrsf.rotateZ(math.pi) # rotate around the z-axis |
|||
aMirroredWire=aWire.copy() |
|||
aMirroredWire.transformShape(aTrsf) |
|||
myWireProfile=Part.Wire([aWire, aMirroredWire]) |
|||
}} |
|||
Do tej pory zbudowaliśmy tylko połowę profilu. Zamiast budować cały profil w ten sam sposób, możemy po prostu zrobić lustrzane odbicie tego, co zrobiliśmy i skleić obie połówki. Najpierw utworzymy macierz. Macierz jest bardzo popularnym sposobem na zastosowanie transformacji do obiektów w świecie 3D, ponieważ może ona zawierać w jednej strukturze wszystkie podstawowe transformacje, jakim mogą podlegać obiekty 3D ''(przesuwanie, obracanie i skalowanie)''. |
|||
Po utworzeniu macierzy odbijamy ją w lustrze, następnie tworzymy kopię naszej linii łamanej i nakładamy na nią macierz transformacji. Mamy teraz już dwie linie, z których możemy utworzyć trzecią, gdyż linie to tak naprawdę listy krawędzi. |
|||
{{Code|code= |
|||
... |
|||
myFaceProfile=Part.Face(myWireProfile) |
|||
aPrismVec=App.Vector(0, 0, myHeight) |
|||
myBody=myFaceProfile.extrude(aPrismVec) |
|||
myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges) |
|||
}} |
|||
Teraz, gdy mamy już zamkniętą linię łamaną, można ją przekształcić w ścianę. Gdy mamy już ścianę, możemy ją wyciągnąć. W ten sposób tworzymy bryłę. Następnie nakładamy na nasz obiekt małe, ładne zaokrąglenie, ponieważ zależy nam na dobrym projekcie, prawda? |
|||
{{Code|code= |
|||
... |
|||
neckLocation=App.Vector(0, 0, myHeight) |
|||
neckNormal=App.Vector(0, 0, 1) |
|||
myNeckRadius = myThickness / 4. |
|||
myNeckHeight = myHeight / 10. |
|||
myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal) |
|||
}} |
|||
W tym momencie korpus naszej butelki jest już gotowy, ale musimy jeszcze stworzyć szyjkę. Tworzymy więc nową bryłę, z walcem. |
|||
{{Code|code= |
|||
... |
|||
myBody = myBody.fuse(myNeck) |
|||
}} |
|||
Obsługa operacji scalenia jest bardzo wydajna. Zajmie się sklejaniem tego, co trzeba skleić i usuwaniem części, które trzeba usunąć. |
|||
{{Code|code= |
|||
... |
|||
return myBody |
|||
}} |
|||
Następnie zwracamy naszą bryłę typu Część jako wynik naszej funkcji. |
|||
{{Code|code= |
|||
el = makeBottleTut() |
|||
Part.show(el) |
|||
}} |
|||
Na koniec wywołujemy funkcję, aby faktycznie utworzyć część, a następnie uczynić ją widoczną. |
|||
{{Top}} |
|||
<span id="Example:_Pierced_box"></span> |
|||
==Przykład: Sześcian z otworami== |
|||
Oto kompletny przykład budowy sześcianu z otworami. |
|||
Konstrukcja jest wykonywana po jednym boku na raz. Kiedy kostka jest gotowa, zostaje wydrążona przez wycięcie w niej walca. |
|||
{{Code|code= |
|||
import FreeCAD as App |
|||
import Part, math |
|||
size = 10 |
size = 10 |
||
poly = Part.makePolygon( |
poly = Part.makePolygon([(0, 0, 0), (size, 0, 0), (size, 0, size), (0, 0, size), (0, 0, 0)]) |
||
face1 = Part.Face(poly) |
face1 = Part.Face(poly) |
||
| Line 752: | Line 886: | ||
face6 = Part.Face(poly) |
face6 = Part.Face(poly) |
||
myMat = |
myMat = App.Matrix() |
||
myMat.rotateZ(math.pi/2) |
|||
myMat.rotateZ(math.pi / 2) |
|||
face2.transformShape(myMat) |
face2.transformShape(myMat) |
||
face2.translate( |
face2.translate(App.Vector(size, 0, 0)) |
||
myMat.rotateZ(math.pi/2) |
myMat.rotateZ(math.pi / 2) |
||
face3.transformShape(myMat) |
face3.transformShape(myMat) |
||
face3.translate( |
face3.translate(App.Vector(size, size, 0)) |
||
myMat.rotateZ(math.pi/2) |
myMat.rotateZ(math.pi / 2) |
||
face4.transformShape(myMat) |
face4.transformShape(myMat) |
||
face4.translate( |
face4.translate(App.Vector(0, size, 0)) |
||
myMat = App.Matrix() |
|||
myMat |
myMat.rotateX(-math.pi / 2) |
||
myMat.rotateX(-math.pi/2) |
|||
face5.transformShape(myMat) |
face5.transformShape(myMat) |
||
face6.transformShape(myMat) |
face6.transformShape(myMat) |
||
face6.translate( |
face6.translate(App.Vector(0, 0, size)) |
||
myShell = Part.makeShell([face1,face2,face3,face4,face5,face6]) |
|||
myShell = Part.makeShell([face1, face2, face3, face4, face5, face6]) |
|||
mySolid = Part.makeSolid(myShell) |
mySolid = Part.makeSolid(myShell) |
||
mySolidRev = mySolid.copy() |
|||
mySolidRev.reverse() |
|||
myCyl = Part.makeCylinder(2,20) |
myCyl = Part.makeCylinder(2, 20) |
||
myCyl.translate( |
myCyl.translate(App.Vector(size / 2, size / 2, 0)) |
||
cut_part = |
cut_part = mySolid.cut(myCyl) |
||
Part.show(cut_part) |
Part.show(cut_part) |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
== Loading and Saving == |
|||
<span id="Loading_and_saving"></span> |
|||
There are several ways to save your work in the Part module. You can |
|||
==Wczytywanie i zapisywanie== |
|||
of course save your FreeCAD document, but you can also save Part |
|||
objects directly to common CAD formats, such as BREP, IGS, STEP and STL. |
|||
Jest kilka sposobów na zapisanie swojej pracy. Możesz oczywiście zapisać swój dokument FreeCAD, ale możesz również zapisać obiekty typu [[Part_Workbench/pl|Część]] bezpośrednio do popularnych formatów CAD, takich jak BREP, IGS, STEP i STL. |
|||
Saving a shape to a file is easy. There are exportBrep(), exportIges(), |
|||
exportStl() and exportStep() methods availables for all shape objects. |
|||
Zapisywanie kształtu do pliku jest łatwe. Dla wszystkich obiektów kształtu dostępne są metody {{incode|exportBrep()}}, {{incode|exportIges()}}, {{incode|exportStep()}} oraz {{incode|exportStl()}}. |
|||
So, doing: |
|||
Tak więc, wykonując: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
import Part |
import Part |
||
s = Part.makeBox( |
s = Part.makeBox(10, 10, 10) |
||
s.exportStep("test.stp") |
s.exportStep("test.stp") |
||
}} |
|||
</syntaxhighlight> |
|||
this will save our box into a STEP file. To load a BREP, |
|||
zapisze naszą kostkę do pliku STEP. Aby wczytać plik BREP, IGES lub STEP: |
|||
IGES or STEP file, simply do the contrary: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
import Part |
import Part |
||
s = Part.Shape() |
s = Part.Shape() |
||
s.read("test.stp") |
s.read("test.stp") |
||
}} |
|||
</syntaxhighlight> |
|||
To convert an '''.stp''' in '''.igs''' file simply : |
|||
Aby przekonwertować plik STEP na plik IGS: |
|||
<syntaxhighlight> |
|||
{{Code|code= |
|||
import Part |
import Part |
||
s = Part.Shape() |
s = Part.Shape() |
||
s.read("file.stp") # incoming file igs, stp, stl, brep |
s.read("file.stp") # incoming file igs, stp, stl, brep |
||
s.exportIges("file.igs") # outbound file igs |
s.exportIges("file.igs") # outbound file igs |
||
}} |
|||
</syntaxhighlight> |
|||
{{Top}} |
|||
Note that importing or opening BREP, IGES or STEP files can also be done |
|||
directly from the File -> Open or File -> Import menu, while exporting |
|||
is with File -> Export |
|||
{{Docnav/pl |
|||
{{docnav|Mesh Scripting|Mesh to Part}} |
|||
|[[FreeCAD_Scripting_Basics/pl|Podstawy tworzenia skryptów FreeCAD]] |
|||
|[[Mesh_Scripting/pl|Skrytpy w Środowisku Siatek]] |
|||
}} |
|||
{{Powerdocnavi{{#translation:}}}} |
|||
[[Category:Poweruser Documentation/pl]] [[Category:Python Code/pl]] [[Category:Tutorials/pl]] |
|||
[[Category:Developer Documentation{{#translation:}}]] |
|||
[[Category:Python Code{{#translation:}}]] |
|||
{{clear}} |
|||
<languages/> |
|||
Latest revision as of 07:12, 15 October 2023
Wprowadzenie
Tutaj wyjaśnimy Ci jak kontrolować środowisko Część bezpośrednio z interpretera FreeCAD Python, lub z dowolnego zewnętrznego skryptu. Przejrzyj sekcję o skryptach oraz strony Podstawy tworzenia skryptów FreeCAD, jeśli potrzebujesz więcej informacji na temat działania skryptów Pythona w FreeCAD. Jeśli jesteś początkującym użytkownikiem środowiska Python, dobrze jest najpierw przeczytać Wprowadzenie do środowiska Python.
Zobacz również
Schemat klas
To jest Unified Modeling Language (UML) przegląd najważniejszych klas modułu Część:
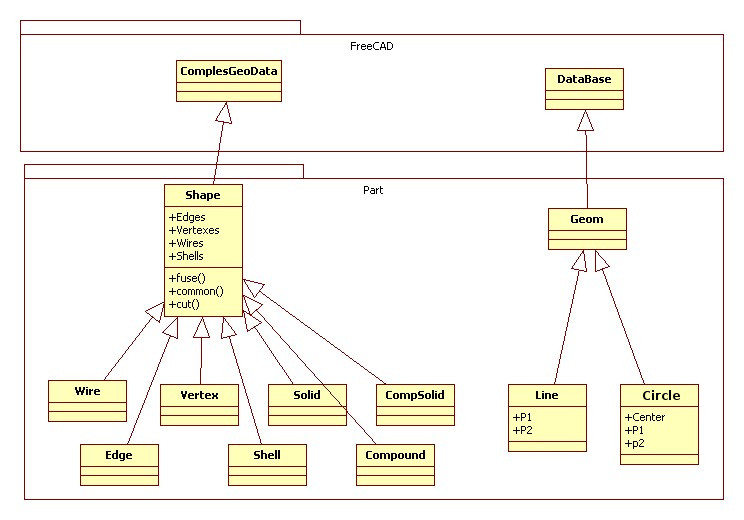
Geometria
Obiekty geometryczne są elementami składowymi wszystkich obiektów topologicznych:
- Geom Klasa bazowa obiektów geometrycznych.
- Linia Linia prosta w przestrzeni 3D, zdefiniowana przez punkt początkowy i punkt końcowy.
- Okrąg Okrąg lub odcinek okręgu zdefiniowany przez punkt środkowy oraz punkt początkowy i końcowy.
- I tak dalej.
Topologia
Dostępne są następujące typy danych topologicznych:
- Złożenie Grupa obiektów topologicznych dowolnego typu.
- Bryła złożona Bryła złożona to zbiór brył połączonych ścianami. Rozszerza pojęcia WIRE i SHELL na bryły.
- Bryła Część przestrzeni ograniczona powłokami. Jest trójwymiarowa.
- Powłoka Zbiór ścian połączonych krawędziami. Powłoka może być otwarta lub zamknięta.
- Ścina W 2D jest częścią płaszczyzny, w 3D jest częścią powierzchni. Jego geometria jest ograniczona (przycięta) przez kontury. Jest dwuwymiarowa.
- Linia łamana (polilinia) Zbiór krawędzi połączonych wierzchołkami. Może to być kontur otwarty lub zamknięty, w zależności od tego, czy krawędzie są połączone, czy nie.
- Krawędź Element topologiczny odpowiadający krzywej ograniczonej. Krawędź jest na ogół ograniczona wierzchołkami. Ma jeden wymiar.
- Wierzchołek Element topologiczny odpowiadający punktowi. Ma zero wymiarów.
- Kształt Termin ogólny obejmujący wszystkie powyższe.
Przykład: Utwórz prostą topologię
Stworzymy teraz topologię poprzez skonstruowanie jej z prostszej geometrii. Jako studium przypadku użyjemy części widocznej na rysunku, która składa się z czterech wierzchołków, dwóch łuków i dwóch linii.
Tworzenie geometrii
Najpierw tworzymy odrębne części geometryczne tej linii łamanej. Upewniamy się, że części, które mają być później połączone, mają wspólne wierzchołki.
Więc najpierw tworzymy punkty:
import FreeCAD as App
import Part
V1 = App.Vector(0, 10, 0)
V2 = App.Vector(30, 10, 0)
V3 = App.Vector(30, -10, 0)
V4 = App.Vector(0, -10, 0)
Łuk
Dla każdego łuku potrzebujemy punktu pomocniczego:
VC1 = App.Vector(-10, 0, 0)
C1 = Part.Arc(V1, VC1, V4)
VC2 = App.Vector(40, 0, 0)
C2 = Part.Arc(V2, VC2, V3)
Linia
Odcinki linii można utworzyć z dwóch punktów:
L1 = Part.LineSegment(V1, V2)
L2 = Part.LineSegment(V3, V4)
Połącz wszystko w całość
Ostatnim krokiem jest zestawienie geometrycznych elementów bazowych razem i uzyskanie kształtu topologicznego:
S1 = Part.Shape([C1, L1, C2, L2])
Utwórz graniastosłup
Teraz wyciągnij linę łamaną w odpowiednim kierunku i stwórz rzeczywisty kształt 3D:
W = Part.Wire(S1.Edges)
P = W.extrude(App.Vector(0, 0, 10))
Pokaż to wszystko
Part.show(P)
Utwórz podstawowe kształty
Możesz łatwo tworzyć podstawowe obiekty topologiczne za pomocą metod make...() z modułu Część:
b = Part.makeBox(100, 100, 100)
Part.show(b)
Niektóre dostępne metody make...():
makeBox(l, w, h, [p, d])Tworzy sześcian znajdujący się w punkcie p i skierowany w kierunku d o wymiarach (l,w,h).makeCircle(radius)Tworzy okrąg o zadanym promieniu.makeCone(radius1, radius2, height). Tworzy stożek o podanych promieniach i wysokościach.makeCylinder(radius, height). Tworzy walec o zadanym promieniu i wysokości.makeLine((x1, y1, z1), (x2, y2, z2))Tworzy prostą z dwóch punktów.makePlane(length, width)Tworzy płaszczyznę o określonej długości i szerokości.makePolygon(list)makePolygon(list)Tworzy wielokąt z listy punktów.makeSphere(radius)Tworzy sferę o zadanym promieniu.makeTorus(radius1, radius2)Tworzy torus o podanych promieniach.
Zobacz stronę skrypty środowiska Część lub dokumentacja API środowiska Część generowana automatycznie aby zobaczyć pełną listę dostępnych metod modułu Część.
Import modułów
Najpierw musimy zaimportować moduły FreeCAD i Część, aby móc korzystać z ich zawartości w Pythonie:
import FreeCAD as App
import Part
Utwórz wektor
Wektory są jedną z najważniejszych informacji przy tworzeniu kształtów. Zazwyczaj zawierają trzy liczby (ale niekoniecznie zawsze): współrzędne kartezjańskie X, Y i Z. Tworzysz wektor w ten sposób:
myVector = App.Vector(3, 2, 0)
Właśnie utworzyliśmy wektor o współrzędnych X = 3, Y = 2, Z = 0. W module Part, wektory są używane wszędzie. Kształty części używają również innego rodzaju reprezentacji punktów zwanej Vertex, która jest po prostu kontenerem dla wektora. Dostęp do wektora wierzchołka uzyskujesz w następujący sposób:
myVertex = myShape.Vertexes[0]
print(myVertex.Point)
> Vector (3, 2, 0)
Utwórz krawędź
Krawędź to nic innego jak linia z dwoma wierzchołkami:
edge = Part.makeLine((0, 0, 0), (10, 0, 0))
edge.Vertexes
> [<Vertex object at 01877430>, <Vertex object at 014888E0>]
Uwaga: Możesz również utworzyć krawędź poprzez przekazanie dwóch wektorów:
vec1 = App.Vector(0, 0, 0)
vec2 = App.Vector(10, 0, 0)
line = Part.LineSegment(vec1, vec2)
edge = line.toShape()
Możesz znaleźć długość i środek krawędzi w ten sposób:
edge.Length
> 10.0
edge.CenterOfMass
> Vector (5, 0, 0)
Wyświetl kształt na ekranie
Do tej pory utworzyliśmy obiekt krawędziowy, ale nie pojawia się on nigdzie na ekranie. Dzieje się tak dlatego, że scena 3D FreeCAD wyświetla tylko to, co każesz jej wyświetlić. Aby to zrobić, użyjemy prostej metody:
Part.show(edge)
Funkcja show tworzy obiekt w naszym dokumencie FreeCAD i przypisuje mu nasz kształt "krawędzi". Używaj jej zawsze wtedy, gdy chcesz wyświetlić swoje dzieło na ekranie.
Utwórz linie łamaną
Linia łamana jest linią o wielu krawędziach i może być utworzona z listy krawędzi lub nawet z listy linii łamanych:
edge1 = Part.makeLine((0, 0, 0), (10, 0, 0))
edge2 = Part.makeLine((10, 0, 0), (10, 10, 0))
wire1 = Part.Wire([edge1, edge2])
edge3 = Part.makeLine((10, 10, 0), (0, 10, 0))
edge4 = Part.makeLine((0, 10, 0), (0, 0, 0))
wire2 = Part.Wire([edge3, edge4])
wire3 = Part.Wire([wire1, wire2])
wire3.Edges
> [<Edge object at 016695F8>, <Edge object at 0197AED8>, <Edge object at 01828B20>, <Edge object at 0190A788>]
Part.show(wire3)
Part.show(wire3) wyświetli 4 krawędzie, z których składa się nasza linia łamana. Inne przydatne informacje mogą być łatwo pobrane:
wire3.Length
> 40.0
wire3.CenterOfMass
> Vector (5, 5, 0)
wire3.isClosed()
> True
wire2.isClosed()
> False
Utwórz ścianę
Tylko ściany utworzone z linii łamanych będą poprawne. W tym przykładzie linia łamana3 jest zamknięta, ale linia łamana2 nie jest (patrz wyżej):
face = Part.Face(wire3)
face.Area
> 99.99999999999999
face.CenterOfMass
> Vector (5, 5, 0)
face.Length
> 40.0
face.isValid()
> True
sface = Part.Face(wire2)
sface.isValid()
> False
Tylko twarze będą posiadać obszar, linie łamane i krawędzie nie.
Utwórz okrąg
Okrąg może być utworzony w ten sposób:
circle = Part.makeCircle(10)
circle.Curve
> Circle (Radius : 10, Position : (0, 0, 0), Direction : (0, 0, 1))
Jeśli chcesz utworzyć go w określonej pozycji i z określonym kierunkiem:
ccircle = Part.makeCircle(10, App.Vector(10, 0, 0), App.Vector(1, 0, 0))
ccircle.Curve
> Circle (Radius : 10, Position : (10, 0, 0), Direction : (1, 0, 0))
okrąg zostanie utworzony w odległości 10 od początku X i będzie skierowany na zewnątrz wzdłuż osi X. Uwaga: makeCircle() akceptuje tylko App.Vector() dla parametrów position i parametry jako wektory normalne, a nie krotki. Możesz również utworzyć część okręgu przez podanie kąta początkowego i końcowego:
from math import pi
arc1 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180)
arc2 = Part.makeCircle(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 180, 360)
Kąty powinny być podane w stopniach. Jeśli masz radiany, po prostu przekonwertuj je za pomocą wzoru:
degrees = radians * 180/pi lub za pomocą modułu math Pythona:
import math
degrees = math.degrees(radians)
Utwórz łuk wzdłuż punktów
Niestety nie ma funkcji makeArc(), ale mamy funkcję Part.Arc() do tworzenia łuku przez trzy punkty. Tworzy ona obiekt łuku łączący punkt początkowy z punktem końcowym przez punkt środkowy. Funkcja toShape() obiektu arc musi zostać wywołana, aby otrzymać obiekt krawędzi, tak samo jak w przypadku użycia Part.LineSegment zamiast Part.makeLine.
arc = Part.Arc(App.Vector(0, 0, 0), App.Vector(0, 5, 0), App.Vector(5, 5, 0))
arc
> <Arc object>
arc_edge = arc.toShape()
Part.show(arc_edge)
Funkcja Arc() akceptuje tylko App.Vector() dla punktów, a nie dla krotek. Możesz również uzyskać łuk używając części okręgu:
from math import pi
circle = Part.Circle(App.Vector(0, 0, 0), App.Vector(0, 0, 1), 10)
arc = Part.Arc(circle,0,pi)
Łuki są poprawnymi krawędziami, tak jak linie, więc mogą być również używane w poliliniach.
Utwórz wielokąt
Wielokąt jest po prostu polilinią o wielu prostych krawędziach. Funkcja makePolygon() przyjmuje listę punktów i tworzy polilinię przechodzącą przez te punkty:
lshape_wire = Part.makePolygon([App.Vector(0, 5, 0), App.Vector(0, 0, 0), App.Vector(5, 0, 0)])
Utwórz krzywą Béziera
Krzywe Béziera są używane do modelowania gładkich krzywych przy użyciu serii biegunów (punktów) i opcjonalnych wag. Poniższa funkcja tworzy krzywą Part.BezierCurve() z serii punktów FreeCAD.Vector(). Uwaga: przy "pobieraniu" i "ustawianiu" pojedynczego bieguna lub wagi, indeksy zaczynają się od 1, a nie od 0.
def makeBCurveEdge(Points):
geomCurve = Part.BezierCurve()
geomCurve.setPoles(Points)
edge = Part.Edge(geomCurve)
return(edge)
Utwórz płaszczyznę
Płaszczyzna jest płaską prostokątną powierzchnią. Metoda używana do jej utworzenia to makePlane(length, width, [start_pnt, dir_normal]). Domyślnie start_pnt = Vector(0, 0, 0) i dir_normal = Vector(0, 0, 1). Użycie dir_normal = Vector(0, 0, 1) spowoduje utworzenie płaszczyzny zwróconej w dodatnim kierunku osi Z, natomiast dir_normal = Vector(1, 0, 0) utworzy płaszczyznę zwróconą w dodatnim kierunku osi X:
plane = Part.makePlane(2, 2)
plane
> <Face object at 028AF990>
plane = Part.makePlane(2, 2, App.Vector(3, 0, 0), App.Vector(0, 1, 0))
plane.BoundBox
> BoundBox (3, 0, 0, 5, 0, 2)
BoundBox jest prostopadłościanem zamykającym płaszczyznę o przekątnej zaczynającej się w punkcie (3, 0, 0) i kończącej w punkcie (5, 0, 2). W tym przypadku grubość BoundBox wzdłuż osi Y wynosi zero, ponieważ nasz kształt jest całkowicie płaski.
Uwaga: makePlane() akceptuje tylko App.Vector() dla start_pnt i dir_normal, a nie krotki.
Utwórz elipsę
Istnieje kilka sposobów na utworzenie elipsy:
Part.Ellipse()
Tworzy elipsę o wartości promienia głównego 2 i promienia mniejszego 1, o środku w punkcie (0, 0, 0).
Part.Ellipse(Ellipse)
Tworzy kopię podanej elipsy.
Part.Ellipse(S1, S2, Center)
Tworzy elipsę wyśrodkowaną w punkcie Center, gdzie płaszczyzna elipsy jest określona przez Center, S1 i S2, jej oś główna jest określona przez Center i S1, jej promień główny jest odległością pomiędzy Center i S1, a jej promień mniejszy jest odległością pomiędzy S2 i osią główną.
Part.Ellipse(Center, MajorRadius, MinorRadius)
Tworzy elipsę o promieniach MajorRadius i MinorRadius, znajdującą się w płaszczyźnie zdefiniowanej przez środek i normalną (0, 0, 1).
eli = Part.Ellipse(App.Vector(10, 0, 0), App.Vector(0, 5, 0), App.Vector(0, 0, 0))
Part.show(eli.toShape())
W powyższym kodzie przekazaliśmy S1, S2 i środek. Podobnie jak Arc, Ellipse tworzy obiekt elipsy, a nie krawędzi, więc musimy go przekonwertować na krawędź używając toShape() do wyświetlenia.
Uwaga: Ellipse() akceptuje tylko App.Vector() dla punktów, a nie dla krotek.
eli = Part.Ellipse(App.Vector(0, 0, 0), 10, 5)
Part.show(eli.toShape())
Dla powyższego konstruktora elipsy przekazaliśmy center, MajorRadius oraz MinorRadius.
Utwórz torusa
Używając makeTorus(radius1, radius2, [pnt, dir, angle1, angle2, angle]).
Domyślnie pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1), angle1 = 0, angle2 = 360 i angle = 360.
Rozważmy torus jako małe koło, które porusza się po dużym okręgu. Radius1 jest promieniem dużego okręgu, radius2 jest promieniem małego okręgu, pnt jest środkiem torusa, a dir jest kierunkiem normalnej. angle1 i angle2 są kątami w stopniach dla małego okręgu; ostatni parametr angle jest po to, by zrobić przekrój torusa:
torus = Part.makeTorus(10, 2)
Powyższy kod utworzy torus o średnicy 20 (promień 10) i grubości 4 (promień małego okręgu 2)
tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 180)
Powyższy kod utworzy wycinek torusa.
tor=Part.makeTorus(10, 5, App.Vector(0, 0, 0), App.Vector(0, 0, 1), 0, 360, 180)
Powyższy kod utworzy połowę torusa; tylko ostatni parametr jest zmieniony, tzn. pozostałe kąty są domyślne. Nadanie kąta 180 spowoduje utworzenie torusa od 0 do 180, czyli jego połowę.
Utwórz sześcian lub prostopadłościan
Przy użyciu makeBox(length, width, height, [pnt, dir]).
Domyślnie pnt = Vector(0, 0, 0) i dir = Vector(0, 0, 1).
box = Part.makeBox(10, 10, 10)
len(box.Vertexes)
> 8
Utwórz sferę
Przy użyciu makeSphere(radius, [pnt, dir, angle1, angle2, angle3]). Domyślnie pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1), angle1 = -90, angle2 = 90 i angle3 = 360.
Kąt1 i kąt2 to pionowe minimum i maksimum sfery, kąt3 to średnica sfery.
sphere = Part.makeSphere(10)
hemisphere = Part.makeSphere(10, App.Vector(0, 0, 0), App.Vector(0, 0, 1), -90, 90, 180)
Utwórz walec
Przy użyciu makeCylinder(radius, height, [pnt, dir, angle]). Domyślnie pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1) i angle = 360.
cylinder = Part.makeCylinder(5, 20)
partCylinder = Part.makeCylinder(5, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180)
Utwórz stożek
Przy użyciu makeCone(radius1, radius2, height, [pnt, dir, angle]). Domyślnie pnt = Vector(0, 0, 0), dir = Vector(0, 0, 1) i angle = 360.
cone = Part.makeCone(10, 0, 20)
semicone = Part.makeCone(10, 0, 20, App.Vector(20, 0, 0), App.Vector(0, 0, 1), 180)
Modyfikuj kształty
Kształty można modyfikować na kilka sposobów. Niektóre z nich to proste operacje przekształcania, takie jak przesuwanie lub obracanie kształtów, inne są bardziej złożone, np. łączenie i odejmowanie jednego kształtu od drugiego.
Operacje przekształcenia
Przekształcanie kształtu
Przesunięcie to czynność polegająca na przeniesieniu kształtu z jednego miejsca w drugie. Każdy kształt (krawędź, ściana, sześcian, itd...) może być przesunięty w ten sam sposób:
myShape = Part.makeBox(2, 2, 2)
myShape.translate(App.Vector(2, 0, 0))
Spowoduje to przesunięcie naszego kształtu "myShape" o 2 jednostki w kierunku X.
Obrót kształtu
Aby obrócić kształt, należy określić środek obrotu, oś i kąt obrotu:
myShape.rotate(App.Vector(0, 0, 0),App.Vector(0, 0, 1), 180)
Powyższy kod obróci kształt o 180 stopni wokół osi Z.
Przekształcenia macierzowe
Macierz jest bardzo wygodnym sposobem przechowywania przekształceń w świecie 3D. W pojedynczej macierzy można ustawić wartości przesunięcia, obrotu i skalowania, które mają być zastosowane do obiektu. Na przykład:
myMat = App.Matrix()
myMat.move(App.Vector(2, 0, 0))
myMat.rotateZ(math.pi/2)
Uwaga: Macierze FreeCAD działają w radianach. Ponadto, prawie wszystkie operacje na macierzach, które przyjmują wektor, mogą również przyjmować trzy liczby, więc te dwie linie robią to samo:
myMat.move(2, 0, 0)
myMat.move(App.Vector(2, 0, 0))
Kiedy nasza macierz jest już ustalona, możemy ją zastosować do naszego kształtu. FreeCAD udostępnia dwie metody, aby to zrobić: transformShape() oraz transformGeometry(). Różnica jest taka, że w przypadku pierwszej z nich mamy pewność, że nie wystąpią żadne deformacje (patrz poniżej Skalowanie kształtu). Naszą transformację możemy zastosować w ten sposób:
myShape.transformShape(myMat)
lub
myShape.transformGeometry(myMat)
Skalowanie kształtu
Skalowanie kształtu jest bardziej niebezpieczną operacją, ponieważ w przeciwieństwie do przesunięcia czy obrotu, skalowanie nierównomierne (z różnymi wartościami dla X, Y i Z) może zmienić strukturę kształtu. Na przykład, skalowanie koła z większą wartością w poziomie niż w pionie przekształci je w elipsę, która zachowuje się matematycznie zupełnie inaczej. Do skalowania nie możemy użyć metody transformShape(), musimy użyć transformGeometry():
myMat = App.Matrix()
myMat.scale(2, 1, 1)
myShape=myShape.transformGeometry(myMat)
Operacje logiczne
Operacja odjęcia
Odejmowanie kształtu od innego nazywane jest w FreeCAD "cięciem" i odbywa się w następujący sposób:
cylinder = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
sphere = Part.makeSphere(5, App.Vector(5, 0, 0))
diff = cylinder.cut(sphere)
Przecięcie
W ten sam sposób przecięcie dwóch kształtów nazywane jest "częścią wspólną" i jest wykonywane w ten sposób:
cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
common = cylinder1.common(cylinder2)
Połączenie
Połączenie nazywa się "scaleniem" i działa w ten sam sposób:
cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
fuse = cylinder1.fuse(cylinder2)
Przekrój
"Przekrój" jest punktem przecięcia bryły z płaszczyzną. Zwraca krzywą przecięcia, krzywą złożoną utworzoną z krawędzi.
cylinder1 = Part.makeCylinder(3, 10, App.Vector(0, 0, 0), App.Vector(1, 0, 0))
cylinder2 = Part.makeCylinder(3, 10, App.Vector(5, 0, -5), App.Vector(0, 0, 1))
section = cylinder1.section(cylinder2)
section.Wires
> []
section.Edges
> [<Edge object at 0D87CFE8>, <Edge object at 019564F8>, <Edge object at 0D998458>,
<Edge object at 0D86DE18>, <Edge object at 0D9B8E80>, <Edge object at 012A3640>,
<Edge object at 0D8F4BB0>]
Wyciąganie
Wyciąganie to czynność "wypychania" płaskiego kształtu w określonym kierunku, w wyniku czego powstaje pełna bryła. Pomyśl o kole, które staje się rurką poprzez "wypychanie" go na zewnątrz:
circle = Part.makeCircle(10)
tube = circle.extrude(App.Vector(0, 0, 2))
Jeśli twój okrąg jest pusty, otrzymasz pustą rurkę. Jeśli twój okrąg jest w rzeczywistości dyskiem z wypełnioną powierzchnią, otrzymasz pełny walec:
wire = Part.Wire(circle)
disc = Part.Face(wire)
cylinder = disc.extrude(App.Vector(0, 0, 2))
Badanie kształtów
Możesz łatwo zbadać topologiczną strukturę danych:
import Part
b = Part.makeBox(100, 100, 100)
b.Wires
w = b.Wires[0]
w
w.Wires
w.Vertexes
Part.show(w)
w.Edges
e = w.Edges[0]
e.Vertexes
v = e.Vertexes[0]
v.Point
Wpisując powyższe linie w interpreterze Python, uzyskasz dobre zrozumienie struktury obiektów Część. Tutaj, nasze polecenie makeBox() utworzyło bryłę. Ta bryła, jak wszystkie bryły typu Część, zawiera ściany. Ściany zawsze zawierają linie łamane (polilinie), które są listą krawędzi ograniczających daną ścianę. Każda ściana ma co najmniej jedną zamkniętą linię łamaną (może mieć ich więcej, jeśli posiada otwór). W liniach łamanych możemy oglądać każdą krawędź z osobna, a wewnątrz każdej krawędzi możemy zobaczyć wierzchołki. Proste krawędzie mają oczywiście tylko dwa wierzchołki.
Analiza krawędzi
W przypadku krawędzi, która jest arbitralną krzywą, najprawdopodobniej chcesz dokonać dyskretyzacji. W FreeCAD krawędzie są parametryzowane przez ich długości. Oznacza to, że możesz przejść po krawędzi/krzywej przez jej długość:
import Part
box = Part.makeBox(100, 100, 100)
anEdge = box.Edges[0]
print(anEdge.Length)
Teraz możesz uzyskać dostęp do wielu właściwości krawędzi, używając długości jako pozycji. Oznacza to, że jeśli krawędź ma długość 100mm, to pozycja początkowa wynosi 0, a końcowa 100.
anEdge.tangentAt(0.0) # tangent direction at the beginning
anEdge.valueAt(0.0) # Point at the beginning
anEdge.valueAt(100.0) # Point at the end of the edge
anEdge.derivative1At(50.0) # first derivative of the curve in the middle
anEdge.derivative2At(50.0) # second derivative of the curve in the middle
anEdge.derivative3At(50.0) # third derivative of the curve in the middle
anEdge.centerOfCurvatureAt(50) # center of the curvature for that position
anEdge.curvatureAt(50.0) # the curvature
anEdge.normalAt(50) # normal vector at that position (if defined)
Użycie zaznaczenia
Tutaj widzimy teraz, jak możemy wykorzystać wybór, który użytkownik przeprowadził w przeglądarce. Najpierw tworzymy sześcian i pokazujemy go w przeglądarce.
import Part
Part.show(Part.makeBox(100, 100, 100))
Gui.SendMsgToActiveView("ViewFit")
Teraz wybierz kilka ścian lub krawędzi. Za pomocą tego skryptu możesz przejść po wszystkich zaznaczonych obiektach i ich elementach podrzędnych:
for o in Gui.Selection.getSelectionEx():
print(o.ObjectName)
for s in o.SubElementNames:
print("name: ", s)
for s in o.SubObjects:
print("object: ", s)
Wybierz kilka krawędzi, a ten skrypt obliczy ich długość:
length = 0.0
for o in Gui.Selection.getSelectionEx():
for s in o.SubObjects:
length += s.Length
print("Length of the selected edges: ", length)
Przykład: Butelka OCC
Typowym przykładem, który można znaleźć na stronie OpenCasCade Technology jest sposób na zbudowanie butelki. Jest to dobre ćwiczenie również dla programu FreeCAD. W rzeczywistości, jeśli będziesz śledził nasz przykład poniżej i stronę OCC jednocześnie, zobaczysz jak dobrze struktury OCC są zaimplementowane w FreeCAD. Skrypt jest dołączony do instalacji FreeCAD (w folderze Mod/Part) i może być wywołany z interpretera Python przez wpisanie:
import Part
import MakeBottle
bottle = MakeBottle.makeBottle()
Part.show(bottle)
Skrypt
Na potrzeby tego poradnika rozważymy okrojoną wersję skryptu. W tej wersji butelka nie będzie wydrążona, a szyjka butelki nie będzie gwintowana.
import FreeCAD as App
import Part, math
def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0):
aPnt1=App.Vector(-myWidth / 2., 0, 0)
aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0)
aPnt3=App.Vector(0, -myThickness / 2., 0)
aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0)
aPnt5=App.Vector(myWidth / 2., 0, 0)
aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4)
aSegment1=Part.LineSegment(aPnt1, aPnt2)
aSegment2=Part.LineSegment(aPnt4, aPnt5)
aEdge1=aSegment1.toShape()
aEdge2=aArcOfCircle.toShape()
aEdge3=aSegment2.toShape()
aWire=Part.Wire([aEdge1, aEdge2, aEdge3])
aTrsf=App.Matrix()
aTrsf.rotateZ(math.pi) # rotate around the z-axis
aMirroredWire=aWire.copy()
aMirroredWire.transformShape(aTrsf)
myWireProfile=Part.Wire([aWire, aMirroredWire])
myFaceProfile=Part.Face(myWireProfile)
aPrismVec=App.Vector(0, 0, myHeight)
myBody=myFaceProfile.extrude(aPrismVec)
myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges)
neckLocation=App.Vector(0, 0, myHeight)
neckNormal=App.Vector(0, 0, 1)
myNeckRadius = myThickness / 4.
myNeckHeight = myHeight / 10.
myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal)
myBody = myBody.fuse(myNeck)
return myBody
el = makeBottleTut()
Part.show(el)
Szczegółowe objaśnienia
import FreeCAD as App
import Part, math
Potrzebny nam będzie oczywiście moduł FreeCAD, ale także moduł Part.
def makeBottleTut(myWidth = 50.0, myHeight = 70.0, myThickness = 30.0):
aPnt1=App.Vector(-myWidth / 2., 0, 0)
aPnt2=App.Vector(-myWidth / 2., -myThickness / 4., 0)
aPnt3=App.Vector(0, -myThickness / 2., 0)
aPnt4=App.Vector(myWidth / 2., -myThickness / 4., 0)
aPnt5=App.Vector(myWidth / 2., 0, 0)
Tutaj definiujemy naszą funkcję makeBottleTut. Funkcja ta może być wywołana bez argumentów, tak jak zrobiliśmy to powyżej, w tym przypadku zostaną użyte domyślne wartości dla szerokości, wysokości i grubości. Następnie definiujemy kilka punktów, które zostaną użyte do budowy naszego profilu bazowego.
...
aArcOfCircle = Part.Arc(aPnt2, aPnt3, aPnt4)
aSegment1=Part.LineSegment(aPnt1, aPnt2)
aSegment2=Part.LineSegment(aPnt4, aPnt5)
Tutaj definiujemy geometrię: łuk, złożony z trzech punktów, oraz dwa odcinki linii, złożone z dwóch punktów.
...
aEdge1=aSegment1.toShape()
aEdge2=aArcOfCircle.toShape()
aEdge3=aSegment2.toShape()
aWire=Part.Wire([aEdge1, aEdge2, aEdge3])
Pamiętasz różnicę między geometrią a kształtami? Tutaj budujemy kształty z naszej geometrii konstrukcyjnej. Trzy krawędzie (krawędzie mogą być proste lub zakrzywione), następnie linia łamana wykonana z tych trzech krawędzi.
...
aTrsf=App.Matrix()
aTrsf.rotateZ(math.pi) # rotate around the z-axis
aMirroredWire=aWire.copy()
aMirroredWire.transformShape(aTrsf)
myWireProfile=Part.Wire([aWire, aMirroredWire])
Do tej pory zbudowaliśmy tylko połowę profilu. Zamiast budować cały profil w ten sam sposób, możemy po prostu zrobić lustrzane odbicie tego, co zrobiliśmy i skleić obie połówki. Najpierw utworzymy macierz. Macierz jest bardzo popularnym sposobem na zastosowanie transformacji do obiektów w świecie 3D, ponieważ może ona zawierać w jednej strukturze wszystkie podstawowe transformacje, jakim mogą podlegać obiekty 3D (przesuwanie, obracanie i skalowanie). Po utworzeniu macierzy odbijamy ją w lustrze, następnie tworzymy kopię naszej linii łamanej i nakładamy na nią macierz transformacji. Mamy teraz już dwie linie, z których możemy utworzyć trzecią, gdyż linie to tak naprawdę listy krawędzi.
...
myFaceProfile=Part.Face(myWireProfile)
aPrismVec=App.Vector(0, 0, myHeight)
myBody=myFaceProfile.extrude(aPrismVec)
myBody=myBody.makeFillet(myThickness / 12.0, myBody.Edges)
Teraz, gdy mamy już zamkniętą linię łamaną, można ją przekształcić w ścianę. Gdy mamy już ścianę, możemy ją wyciągnąć. W ten sposób tworzymy bryłę. Następnie nakładamy na nasz obiekt małe, ładne zaokrąglenie, ponieważ zależy nam na dobrym projekcie, prawda?
...
neckLocation=App.Vector(0, 0, myHeight)
neckNormal=App.Vector(0, 0, 1)
myNeckRadius = myThickness / 4.
myNeckHeight = myHeight / 10.
myNeck = Part.makeCylinder(myNeckRadius, myNeckHeight, neckLocation, neckNormal)
W tym momencie korpus naszej butelki jest już gotowy, ale musimy jeszcze stworzyć szyjkę. Tworzymy więc nową bryłę, z walcem.
...
myBody = myBody.fuse(myNeck)
Obsługa operacji scalenia jest bardzo wydajna. Zajmie się sklejaniem tego, co trzeba skleić i usuwaniem części, które trzeba usunąć.
...
return myBody
Następnie zwracamy naszą bryłę typu Część jako wynik naszej funkcji.
el = makeBottleTut()
Part.show(el)
Na koniec wywołujemy funkcję, aby faktycznie utworzyć część, a następnie uczynić ją widoczną.
Przykład: Sześcian z otworami
Oto kompletny przykład budowy sześcianu z otworami.
Konstrukcja jest wykonywana po jednym boku na raz. Kiedy kostka jest gotowa, zostaje wydrążona przez wycięcie w niej walca.
import FreeCAD as App
import Part, math
size = 10
poly = Part.makePolygon([(0, 0, 0), (size, 0, 0), (size, 0, size), (0, 0, size), (0, 0, 0)])
face1 = Part.Face(poly)
face2 = Part.Face(poly)
face3 = Part.Face(poly)
face4 = Part.Face(poly)
face5 = Part.Face(poly)
face6 = Part.Face(poly)
myMat = App.Matrix()
myMat.rotateZ(math.pi / 2)
face2.transformShape(myMat)
face2.translate(App.Vector(size, 0, 0))
myMat.rotateZ(math.pi / 2)
face3.transformShape(myMat)
face3.translate(App.Vector(size, size, 0))
myMat.rotateZ(math.pi / 2)
face4.transformShape(myMat)
face4.translate(App.Vector(0, size, 0))
myMat = App.Matrix()
myMat.rotateX(-math.pi / 2)
face5.transformShape(myMat)
face6.transformShape(myMat)
face6.translate(App.Vector(0, 0, size))
myShell = Part.makeShell([face1, face2, face3, face4, face5, face6])
mySolid = Part.makeSolid(myShell)
myCyl = Part.makeCylinder(2, 20)
myCyl.translate(App.Vector(size / 2, size / 2, 0))
cut_part = mySolid.cut(myCyl)
Part.show(cut_part)
Wczytywanie i zapisywanie
Jest kilka sposobów na zapisanie swojej pracy. Możesz oczywiście zapisać swój dokument FreeCAD, ale możesz również zapisać obiekty typu Część bezpośrednio do popularnych formatów CAD, takich jak BREP, IGS, STEP i STL.
Zapisywanie kształtu do pliku jest łatwe. Dla wszystkich obiektów kształtu dostępne są metody exportBrep(), exportIges(), exportStep() oraz exportStl().
Tak więc, wykonując:
import Part
s = Part.makeBox(10, 10, 10)
s.exportStep("test.stp")
zapisze naszą kostkę do pliku STEP. Aby wczytać plik BREP, IGES lub STEP:
import Part
s = Part.Shape()
s.read("test.stp")
Aby przekonwertować plik STEP na plik IGS:
import Part
s = Part.Shape()
s.read("file.stp") # incoming file igs, stp, stl, brep
s.exportIges("file.igs") # outbound file igs
- Tworzenie skryptów FreeCAD: Python, Wprowadzenie do środowiska Python, Poradnik: Tworzenie skryptów Python, Podstawy tworzenia skryptów FreeCAD
- Moduły: Moduły wbudowane, Jednostki miar, Ilość
- Środowiska pracy: Tworzenie Środowiska pracy, Polecenia Gui, Polecenia, Instalacja większej liczby Środowisk pracy
- Siatki i elementy: Skrytpy w Środowisku Siatek, v, Konwerska Mesh na Part, PythonOCC
- Obiekty parametryczne: Obiekty tworzone skryptami, Obsługa obrazu (Ikonka niestandardowa w widoku drzewa)
- Scenegraph: Coin (Inventor) scenegraph, Pivy
- Interfejs graficzny: Stworzenie interfejsu, Kompletne stworzenie interfejsu w środowisku Python (1, 2, 3, 4, 5), PySide, PySide examples początkujący, średniozaawansowany, zaawansowany
- Makrodefinicje: Makrodefinicje, Instalacja makrodefinicji
- Osadzanie programu: Osadzanie programu FreeCAD, Osadzanie GUI FreeCAD
- Pozostałe: Wyrażenia, Wycinki kodu, Funkcja kreślenia linii, Biblioteka matematyczna FreeCAD dla wektorów (deprecated)
- Węzły użytkowników: Centrum użytkownika, Centrum Power użytkowników, Centrum programisty