Szkicownik: Zmniejsz krotność węzła krzywej złożonej
|
|
| Lokalizacja w menu |
|---|
| Szkic → Narzędzia szkicownika krzywej złożonej → Zwiększ krotność węzła krzywej złożonej |
| Środowisko pracy |
| Szkicownik |
| Domyślny skrót |
| brak |
| Wprowadzono w wersji |
| 0.17 |
| Zobacz także |
| Pokaż / ukryj wyświetlanie węzłów krzywej złożonej, Zwiększ krotność węzła krzywej złożonej |
Opis
Zwiększa stopień (kolejność) krzywej złożonej (zobacz stronę Krzywe złożone aby uzyskać więcej informacji).
Krzywe złożone są w zasadzie kombinacją Krzywych Béziera (ładnie wyjaśnione w filmie From Bézier curves to B-spline curves oraz Properties of B-spline curves).
Punkty, w których dwie krzywe Béziera są połączone, tworząc splajn, nazywamy węzłami. Węzeł na krzywej stopnia d o krotności m oznacza, że krzywa na lewo i prawo od węzła ma co najmniej równą pochodną rzędu n (zwaną Cn ciągłą), podczas gdy .
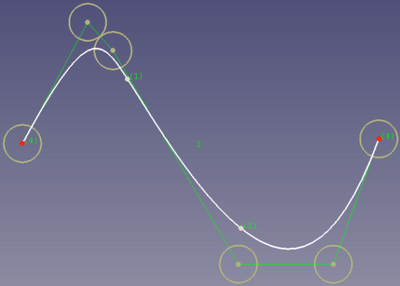
Oto krzywa sześcienna (), której węzły mają krotność 1. Mnogość jest wskazywana przez liczbę w nawiasie. Wskazanie można zmienić za pomocą przycisku na pasku narzędzi Pokaż / ukryj wyświetlanie węzłów krzywej złożonej:
Krzywa złożona gdzie oba węzły mają mnogość 1.
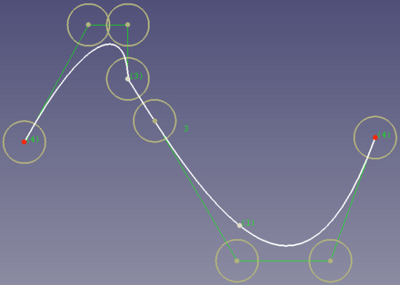
Krotność 3 zmieni tą krzywą tak, że nawet pochodne pierwszego rzędu nie będą równe (C0 ciągłości). Oto ta sama krzywa, w której krotność węzła lewego została zwiększona do 3:
Krzywa złożona z góry z krotnością węzłów 3. Punkt kontrolny został przesunięty, aby pokazać, że węzeł ma ciągłość „C”0.
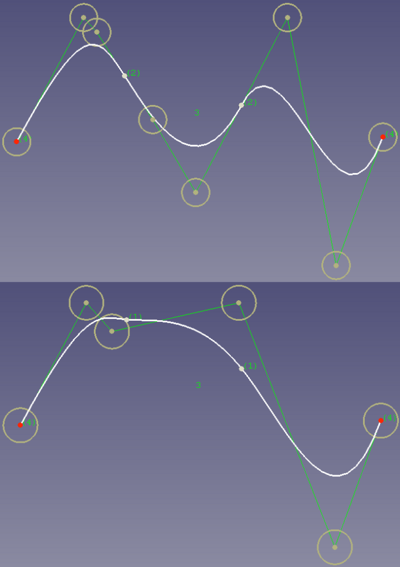
Konsekwencją większej krotności jest to, że za cenę utraty ciągłości zyskujemy lokalną kontrolę. Oznacza to, że zmiana jednego punktu kontrolnego wpływa na krzywą tylko lokalnie do tego zmienionego punktu. Widać to na tym przykładzie, gdzie wzięto krzywą z pierwszego obrazka powyżej i przesunięto w górę jej drugi punkt kontrolny z prawej strony:
Efekt lokalności ze względu na różną krotność.
Można zauważyć, że krzywa z krotnością węzła 1 jest całkowicie zmieniona, natomiast krzywa z krotnością 2 zachowała swoją formę po swojej lewej stronie.
Note: If you decrease the multiplicity, the knot vanishes, because mathematically it appears then zero times in the knot vector, meaning there is no longer a basis function. Understanding this, requires some math, but it will also be clear when you look at the multiplicity: For example degree = 3 then multiplicity = 0 means that at the position of the knot two Bézier pieces are connected with C3 continuity. So the third derivative should be equal on both sides of the knot. However for a cubic Bézier curve (that is a polynom with degree 3) , this means both sides must be part of the same curve. So there is then actually no longer a knot connecting 2 different Bézier curves, the former knot is then simply a point onto one Bézier curve.
Usage
- Select a B-spline knot, either:
- Press the button
Decrease knot multiplicity.
- Use the menu Sketch → Sketcher B-spline tools →
Decrease knot multiplicity.
- Press the button
Note: Decreasing the multiplicity from 1 to 0 will remove the knot since the result would be a curve with an "edge" at the knot position (C0 continuity) and this is not supported. (To create curves with an "edge", you can create two splines and connect them.)
- Przybory: Nowy szkic, Edycja szkicu, Mapuj szkic na powierzchnię, Zmień orientację szkicu, Sprawdź poprawność szkicu, Połącz szkice, Odbicie lustrzane szkicu, Zamknij szkic, Widok szkicu, Widok przekroju, Włącz / wyłącz siatkę, Włącz / wyłącz przyciąganie, Kolejność renderowania, Przerwij operację
- Geometrie szkicownika: Punkt, Linia, Komponent utwórz łuk, Łuk, Utwórz łuk przez 3 punkty, Komponent utwórz okrąg, Okrąg, Utwórz okrąg przez 3 punkty, Komponent utwórz stożek, Utwórz elipsę względem środka, Utwórz elipsę przez 3 punkty, Utwórz łuk elipsy, Utwórz łuk hyperboli, Utwórz łuk paraboli, Komponent utwórz krzywą złożoną, Utwórz krzywą złożoną, Utwórz okresową utwórz krzywą złożoną, Polylinia (linia wielopunktowa), Prostokąt, Komponent utwórz wielokąt foremny, Trójkąt, Kwadrat, Pięciokąt, Sześciokąt, Siedmiokąt, Ośmiokąt, Utwórz wielokąt foremny, Rowek, Zaokrąglenie, Zaokrąglenie z zachowaniem wiązań, Przytnij, Rozszerz, Geometria zewnętrzna, Kalka techniczna, Tryb konstrukcyjny
- Wiązania szkicownika
- Wiązania geometryczne Wiązanie zbieżności punktów, Wiązanie punktu na obiekcie, Wiązanie pionowe, Wiązanie poziome, Wiązanie równoległości, Wiązanie prostopadłości, Wiązanie styczności, Wiązanie równości, Wiązanie symetrii, Wiązanie zablokowania
- Wiązania wymiarów Wiązanie blokady odległości, Zwiąż odległość poziomą, Zwiąż odległość pionową, Wiązanie odległości, Wiązanie promienia, Wiązanie średnicy, Zwiąż automatycznie promień / średnicę, Wiązanie kąta, Wiązanie prawo Snella
- Narzędzia wiązań: Przełącz kontrolę wiązania, Przełącz aktywność wiązania
- Narzędzia szkicownika Wybierz elementy bez wiązań, Wybierz powiązane więzy, Wybierz powiązaną geometrię, Wybierz zbędne wiązania, Wybierz wiązania konfliktowe, Pokaż / ukryj geometrię wewnętrzną, Wybierz odniesienie położenia, Wybierz oś poziomą, Wybierz oś pionową, Odbicie lustrzane, Klonuj, Kopiuj, Przesuń, Szyk prostokątny, Usuń wyrównanie osi, Usuń wszystkie geometrie, Usuń wszystkie wiązania
- Narzędzia B-spline dla szkicownika. Pokaż / ukryj stopień krzywej złożonej, Pokaż/ukryj ramkę kontrolną krzywej złożonej, Pokaż / ukryj grzebień krzywizny krzywej złożonej, Pokaż / ukryj wyświetlanie węzłów krzywej złożonej, Pokaż / ukryj wagę punktu kontrolnego krzywej złożonej, Konwertuj geometrię na krzywą złożoną, Zwiększ stopień krzywej złożonej, Zmniejsz stopień krzywej złożonej, Zwiększ krotność węzłów krzywej złożonej, Zmniejsz krotność węzła krzywej złożonej, Wstaw węzeł, Połącz krzywe
- Przestrzeń wirtualna szkicownika Przełącz przestrzeń wirtualną
- Dodatkowe: Okienko dialogowe Szkicownika, Preferencje, Skrypty Szkicownika
- Jak zacząć
- Instalacja: Pobieranie programu, Windows, Linux, Mac, Dodatkowych komponentów, Docker, AppImage, Ubuntu Snap
- Podstawy: Informacje na temat FreeCAD, Interfejs użytkownika, Profil nawigacji myszką, Metody wyboru, Nazwa obiektu, Edytor ustawień, Środowiska pracy, Struktura dokumentu, Właściwości, Pomóż w rozwoju FreeCAD, Dotacje
- Pomoc: Poradniki, Wideo poradniki
- Środowiska pracy: Strona Startowa, Architektura, Assembly, CAM, Rysunek Roboczy, MES, Inspekcja, Siatka, OpenSCAD, Część, Projekt Części, Punkty, Inżynieria Wsteczna, Robot, Szkicownik, Arkusz Kalkulacyjny, Powierzchnia 3D, Rysunek Techniczny, Test Framework